Project BVVIZ is a tool that provides a user-friendly playground for running noisy quantum simulations and visualizing the Bernstein-Vazirani quantum algorithm.

source: bernstein-vazirani.streamlit.app
The Bernstein-Vazirani protocol is a quantum algorithm introduced in 1992, by computer scientists Ethan Bernstein and Umesh Vazirani. It was shown that there can be advantages in using a quantum computer as a computational tool for more complex problems than the Deutsch-Jozsa problem.
It has a potential use in classical cryptography and quantum key distribution and communication. Shor’s protocol, one of the most popular quantum algorithms - capable of a prime factorization in \( \mathcal{O}( \log{} n ) \), uses many properties of quantum circuits leveraged in this protocol.
The problem
The Bernstein-Vazirani problem is a promise problem. It involves a black-box function \( f_s \colon \{0, 1\}^n \rightarrow \{0, 1\} \), which takes a bit string as input and returns either 0 or 1. The function guarantees to return the dot product between x and a secret string \( s \in \{ 0, 1 \}^n \) modulo 2:
$$ f_s({ x_0, x_1, …, x_{(n-1)} }) = x \cdot s $$ $$ x \cdot s = x_0 s_0 \oplus x_1 s_1 \oplus … \oplus x_{n-1} s_{n-1} $$
The objective is to determine the secret string s of the function \( f_s \).
Solution
The project BVVIZ implements both classical and quantum solutions for the Bernstein-Vazirani algorithm. These solutions are compared in terms of the number of queries made to the oracle function \( f_s \), computational time, accuracy, and overall complexity.

image source: Qiskit
Classical algorithm
The implementation of the classical algorithm finds the secret string by evaluating the function \( f_s \) n-times with the input values \( x = 2^i = 1 \ll i \) for all \( i \in \{0, 1, ..., n-1\} \). By querying the i-th bit, the i-th bit of the secret string is determined.
The project BVVIZ implementation of the classical algorithm is also the most efficient since no more than one bit of information can be revealed by a single query to the oracle. The complexity of the classical approach is \( \mathcal{O}( n ) \).
Quantum algorithm
On the other hand, project BVVIZ’s implementation of the quantum algorithm obtains the hidden secret string with certainty in a single query to the oracle function \( f_s(x) \), resulting in a complexity of \( \mathcal{O}( 1 ) \).
This is achieved by introducing input qubits \( |0 \rangle_n \) into an equal linear superposition of the \( 2^n \) basis states by applying n Hadamard gates. An additional auxiliary qubit, carrying the output bit of information, is set to \( |-\rangle \) using a single Hadamard and Pauli-X gate.
The state ofter applying the quantum oracle function \( f_s \) is
$$ H^{\otimes n} |0\rangle \otimes HX|0\rangle = \frac{1}{\sqrt{2^n}} \sum_{x=0}^{2^{n-1}} |x\rangle \otimes |-\rangle . $$
The oracle function \( f_s \) flips each qubit \( q_i \) that satisfies \( f_s(\text{bin}(2^i)) = 1 \), which changes the sign of these states. This is also known as phase kickback.
Since all quantum gates are their own inverses, n Hadamard gates are applied to obtain the final result:
$$ \frac{1}{\sqrt{2^n}} \sum_{x=0}^{2^{n-1}} (-1)^{s \cdot} \xrightarrow{H^{\otimes n}} |s\rangle $$
Implementation

An implementation of the Bernstein-Vazirani protocol for a secret string 101
The underlying problems of quantum technology are often misunderstood. This tool guides users to understand both benefits and constraints of quantum computing.
Quantum simulation
BVVIZ allows the freedom to customize the simulator device, including the backend system, number of shots, secret string, or their own noise and transpiler model. This enables full control over the quantum hardware that is being simulated to run the Bernstein-Vazirani experiment.

The quantum register mapping of a preconfigured Brooklyn system with sabre layout and stochastic routing
Accuracy assessment
As a result of the quantum simulation, metrics, plots, and charts are generated to help users understand the impact of the noisy quantum devices. It encourages to take a closer look at the experimental settings, analyze the results, think about the statistics, and come up with independent conclusions and their own way of understanding limitations of quantum computing.

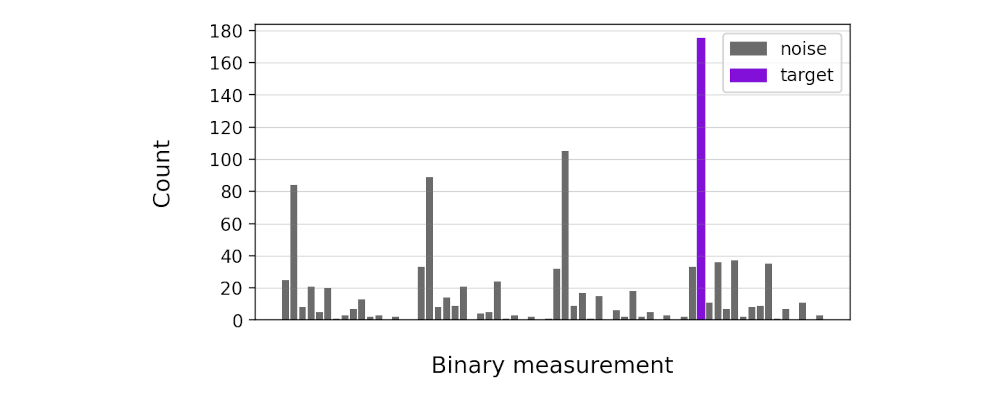
A count chart of an experiment with secret string 11001 and 1000 shots
If the provided statistics are inadequate or lacking, users are free to download the quantum circuit (OpenQASM 2.0) and the measurements.
Purpose
Project BVVIZ helps those who are new to quantum computation not only to learn about the Bernstein-Vazirani algorithm, but also to gain a deeper understanding of the capabilities of quantum technology, which is currently very much limited by the unreliable hardware.

The metrics of an experiment performed on a very noisy device
Conclusion

source: bernstein-vazirani.streamlit.app
The simulation and visualization of the Bernstein-Vazirani protocol works properly and as expected. The application does a decent job of delivering the results.
The project was designed and developed with modularity in mind, allowing for easy expansion. Integrating new metrics, statistics, and plots can be done straightforwardly. With minor adjustments, it could also simulate and visualize other quantum protocols like Simon’s, Deutsch-Jozsa’s, and Grover’s algorithms.
Try it yourself
Feel free to experiment with BVVIZ first hand. The source code is available at github.com/chutommy/bvviz.