This project explores various deep learning approaches to classify images from the Fashion MNIST dataset. We’ll compare different neural network architectures and regularization techniques to identify the most effective model.
import copy
import pathlib
import pickle
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import torch
from matplotlib.ticker import MaxNLocator
from scipy.ndimage import zoom
from sklearn.metrics import ConfusionMatrixDisplay
from sklearn.metrics import RocCurveDisplay
from sklearn.metrics import accuracy_score
from sklearn.metrics import classification_report
from sklearn.model_selection import train_test_split
from torch import nn
from torch.nn.functional import relu
from torch.utils.data import DataLoader
from torch.utils.data import TensorDataset
pd.set_option("display.max_columns", 10)
pd.set_option("display.precision", 3)
plt.style.use("default")
random_state = 42
batch_size = 256
max_epochs = 30
!command -v nvidia-smi &> /dev/null && nvidia-smi
Data Preparation
We start by loading the Fashion MNIST dataset and splitting it into training, validation, and test sets.
workdir = pathlib.Path(".")
train_file = workdir / "train.csv"
eval_file = workdir / "evaluate.csv"
res_file = workdir / "results.csv"
artifacts_path = workdir / "artifacts"
models_path = artifacts_path / "models"
logs_path = artifacts_path / "logs"
outputs_path = artifacts_path / "outputs"
artifacts_path.mkdir(parents=True, exist_ok=True)
models_path.mkdir(parents=True, exist_ok=True)
logs_path.mkdir(parents=True, exist_ok=True)
outputs_path.mkdir(parents=True, exist_ok=True)
df = pd.read_csv(train_file)
display(df.head(5))
cats = [
"T-shirt/top",
"Trouser",
"Pullover",
"Dress",
"Coat",
"Sandal",
"Shirt",
"Sneaker",
"Bag",
"Ankle boot",
]
MAP_IL = {i: c for i, c in enumerate(cats)}
VEC_IL = np.vectorize(MAP_IL.get)
d = df.drop("label", axis=1)
fig, ax = plt.subplots(4, 8, figsize=(10, 6))
fig.suptitle("Sample from training data (inverted brightness)")
for j in range(4):
for i in range(8):
ax[j, i].imshow(d.iloc[5 * j + i].to_numpy().reshape((32, 32)), cmap="Greys")
ax[j, i].set_title(MAP_IL[df.loc[5 * j + i, "label"]], fontsize=11)
ax[j, i].set_axis_off()
plt.show()
| pix1 | pix2 | pix3 | pix4 | pix5 | ... | pix1021 | pix1022 | pix1023 | pix1024 | label | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 | ... | 0 | 0 | 0 | 0 | 3 |
| 1 | 1 | 1 | 1 | 1 | 1 | ... | 1 | 1 | 1 | 1 | 3 |
| 2 | 1 | 1 | 1 | 1 | 1 | ... | 1 | 1 | 1 | 1 | 7 |
| 3 | 0 | 0 | 0 | 0 | 0 | ... | 0 | 0 | 0 | 0 | 9 |
| 4 | 1 | 1 | 1 | 1 | 1 | ... | 1 | 1 | 1 | 1 | 5 |
5 rows × 1025 columns

The dataset consists of 32x32 pixel grayscale images, each belonging to one of 10 clothing categories:
- T-shirt/top
- Trouser
- Pullover
- Dress
- Coat
- Sandal
- Shirt
- Sneaker
- Bag
- Ankle boot
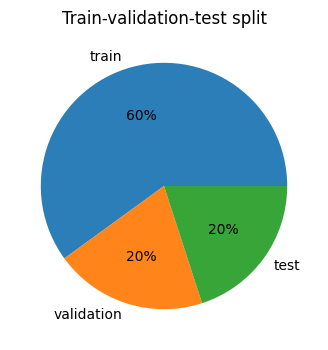
Train-Validation-Test Split
We split the data into training (60%), validation (20%), and test (20%) sets.
X_all = df.drop("label", axis=1).to_numpy(np.uint8)
y_all = df.loc[:, "label"].to_numpy(np.uint8)
X_train_val, X_test, y_train_val, y_test = train_test_split(
X_all, y_all, test_size=0.2, random_state=random_state
)
X_train, X_val, y_train, y_val = train_test_split(
X_train_val, y_train_val, test_size=0.25, random_state=random_state
)
d = pd.DataFrame(
[
["train", X_train.shape[0], X_train.shape[0] / X_all.shape[0]],
["validation", X_val.shape[0], X_val.shape[0] / X_all.shape[0]],
["test", X_test.shape[0], X_test.shape[0] / X_all.shape[0]],
],
columns=["dataset", "count", "relative count"],
)
display(d)
fig, ax = plt.subplots(figsize=(4, 4))
ax.pie(d["count"], labels=d["dataset"], autopct="%1.f%%", wedgeprops={"alpha": 0.95})
ax.set_title("Train-validation-test split")
plt.show()
| dataset | count | relative count | |
|---|---|---|---|
| 0 | train | 31500 | 0.6 |
| 1 | validation | 10500 | 0.2 |
| 2 | test | 10500 | 0.2 |
Exploratory Data Analysis
Let’s examine the features (pixels) and target variable (class).
Features (Pixels)
d = pd.DataFrame(
[
["count", X_train.shape[0]],
["size", X_train.shape[1]],
["min", X_train.min()],
["mean", X_train.mean().astype(int)],
["max", X_train.max()],
],
columns=["stat", "value"],
)
display(d.set_index("stat").T)
d = X_train.flatten()
d2 = pd.DataFrame(
[
["black pixel (lte 10)", d[d <= 10].shape[0]],
["non-black pixel (gt 10)", d[d > 10].shape[0]],
],
columns=["color", "count"],
)
fig, ax = plt.subplots(figsize=(6, 3))
ax.bar(d2["color"], d2["count"])
ax.set_title("Pixel count: black v. non-black")
ax.set_ylabel("count")
plt.show()
d = X_train.flatten()
fig, ax = plt.subplots(figsize=(6, 4))
ax.hist(d[d > 10], bins=20)
ax.set_title("Histogram of gray level distribution (gt 10)")
ax.set_xlabel("grey level")
ax.set_ylabel("frequency")
plt.show()
| stat | count | size | min | mean | max |
|---|---|---|---|---|---|
| value | 31500 | 1024 | 0 | 44 | 255 |
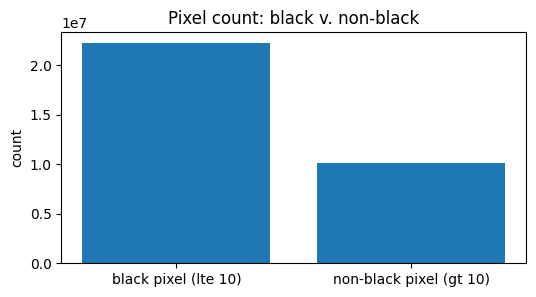
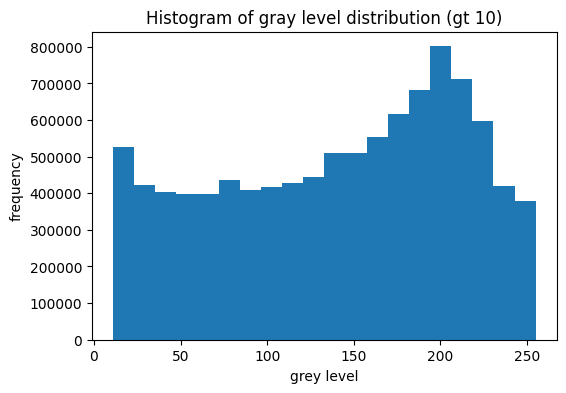
Images are mostly black pixels. Non-black pixels frequently have a brightness around 200.
Target variable (class)
d = []
for c in range(10):
d.append(
[
f"{MAP_IL[c]}",
sum(y_train == c),
round(sum(y_train == c) / y_train.shape[0], 3),
]
)
d = pd.DataFrame(d, columns=["label", "count", "relative count"])
display(d)
fig, ax = plt.subplots(figsize=(4, 4))
ax.pie(
d.loc[:, "count"],
labels=d.loc[:, "label"],
autopct="%.0f%%",
wedgeprops={"alpha": 0.8},
)
ax.set_title("Class distribution")
plt.show()
| label | count | relative count | |
|---|---|---|---|
| 0 | T-shirt/top | 3103 | 0.099 |
| 1 | Trouser | 3052 | 0.097 |
| 2 | Pullover | 3170 | 0.101 |
| 3 | Dress | 3179 | 0.101 |
| 4 | Coat | 3067 | 0.097 |
| 5 | Sandal | 3199 | 0.102 |
| 6 | Shirt | 3137 | 0.100 |
| 7 | Sneaker | 3183 | 0.101 |
| 8 | Bag | 3225 | 0.102 |
| 9 | Ankle boot | 3185 | 0.101 |
Class distribution is balanced. No resampling is needed.
for c in range(10):
fig, ax = plt.subplots(1, 10, figsize=(10, 1.5))
fig.suptitle(f"{MAP_IL[c]}")
d = X_train[y_train == c]
for i in range(10):
ax[i].imshow(d[i].reshape((32, 32)), cmap="Greys")
ax[i].set_axis_off()
plt.show()










Distinguishing between “T-shirt/top” and “Shirt”, or “Pullover” and “Coat”, or “Sneaker” and “Ankle boot” might be challenging for the model.
Data Preprocessing and Augmentation
Image Augmentation
To make the model robust to variations, we augment the data with horizontal flips and zooms.
def augment(x, k):
x1 = np.fliplr(x)
x2 = zoom(x[k : 32 - k, k : 32 - k], 32 / (32 - 2 * k), order=0)
x3 = np.fliplr(x2)
return x1, x2, x3
def data_augment(X, y):
X_aug = np.empty((4 * X.shape[0], X.shape[1]), dtype=np.uint8)
y_aug = np.repeat(y, 4)
for i in range(X.shape[0]):
x0 = X[i].reshape((32, 32))
x1, x2, x3 = augment(x0, 2)
X_aug[4 * i] = x0.flatten()
X_aug[4 * i + 1] = x1.flatten()
X_aug[4 * i + 2] = x2.flatten()
X_aug[4 * i + 3] = x3.flatten()
return X_aug, y_aug
new_X_train, new_y_train = data_augment(X_train, y_train)
new_X_val, new_y_val = data_augment(X_val, y_val)
fig, axes = plt.subplots(5, 4, figsize=(8, 8))
for i in range(5):
x1 = X_train[i].reshape((32, 32))
x2, x3, x4 = augment(x1, k=5)
ax = axes[i]
ax[0].imshow(x1, cmap="Greys")
ax[1].imshow(x2, cmap="Greys")
ax[2].imshow(x3, cmap="Greys")
ax[3].imshow(x4, cmap="Greys")
if i == 0:
ax[0].set_title("original")
ax[1].set_title("flipped")
ax[2].set_title("cropped")
for j in range(4):
ax[j].set_axis_off()
plt.show()

This augmentation helps the model become invariant to image orientation and size.
Data and Device Setup
We prepare the datasets for batch processing and identify the available device (CPU/GPU).
train_dataloader = DataLoader(
TensorDataset(
torch.Tensor(new_X_train).reshape((-1, 1, 32, 32)),
torch.Tensor(new_y_train).type(torch.uint8),
),
batch_size=batch_size,
)
val_dataloader = DataLoader(
TensorDataset(
torch.Tensor(new_X_val).reshape((-1, 1, 32, 32)),
torch.Tensor(new_y_val).type(torch.uint8),
),
batch_size=batch_size,
)
test_dataloader = DataLoader(
TensorDataset(
torch.Tensor(X_test).reshape((-1, 1, 32, 32)),
torch.Tensor(y_test).type(torch.uint8),
),
batch_size=batch_size,
)
for X, y in train_dataloader:
print(f"Shape of X [N, C, H, W]: {X.shape}")
print(f"Shape of y: {y.shape} {y.dtype}")
break
device = (
"cuda"
if torch.cuda.is_available()
else "mps" if torch.backends.mps.is_available() else "cpu"
)
print(f"Using {device} device")
Shape of X [N, C, H, W]: torch.Size([256, 1, 32, 32])
Shape of y: torch.Size([256]) torch.uint8
Using cpu device
Feedforward Neural Networks
Here, we define a set of functions for training neural networks, incorporating early stopping for regularization.
class EarlyStopping:
def __init__(self, tolerance, model):
self.tolerance = tolerance
self.counter = 0
self.early_stop = False
self.init = False
self.max_acc = 0
self.best_model = model
def __call__(self, model, val_acc):
if not self.init:
self.init = True
self.max_acc = val_acc
self.best_model = copy.deepcopy(model)
return
if val_acc > self.max_acc:
self.counter = 0
self.max_acc = val_acc
self.best_model = copy.deepcopy(model)
return
else:
self.counter += 1
if self.counter >= self.tolerance:
self.early_stop = True
return
def train(dataloader, model, loss_fn, optimizer):
size = len(dataloader.dataset)
num_batches = len(dataloader)
model.train()
total_loss, total_correct = 0, 0
for batch, (X, y) in enumerate(dataloader):
X, y = X.to(device), y.to(device)
pred = model(X)
loss = loss_fn(pred, y)
loss.backward()
optimizer.step()
optimizer.zero_grad()
with torch.no_grad():
total_loss += loss.item()
total_correct += (pred.argmax(1) == y).type(torch.float).sum().item()
if batch % 100 == 0:
loss, current = loss.item(), (batch + 1) * len(X)
total_loss /= num_batches
total_correct /= size
return total_correct, total_loss
def test(dataloader, model, loss_fn):
size = len(dataloader.dataset)
num_batches = len(dataloader)
model.eval()
loss, correct = 0, 0
with torch.no_grad():
for X, y in dataloader:
X, y = X.to(device), y.to(device)
pred = model(X)
loss += loss_fn(pred, y).item()
correct += (pred.argmax(1) == y).type(torch.float).sum().item()
loss /= num_batches
correct /= size
print(
f"Validation Error: \n Accuracy: {(100*correct):>0.1f}%, Avg loss: {loss:>8f} \n"
)
return correct, loss
def predict_proba(dataloader, model, out_path):
if out_path.is_file():
return pickle.load(open(out_path, "rb"))
size = len(dataloader.dataset)
y_hat = np.empty((0, 10), dtype=np.uint8)
model.eval()
with torch.no_grad():
for X in dataloader:
X = X[0].to(device)
logits = model(X)
y_hat = np.concatenate((y_hat, logits.cpu()))
pickle.dump(y_hat, open(out_path, "wb"))
return y_hat
def predict(dataloader, model, out_path):
return np.argmax(predict_proba(dataloader, model, out_path), axis=1)
def load_model(file, m):
model_path = models_path / (file + ".pt")
m.load_state_dict(torch.load(model_path, map_location=torch.device(device)))
return m
def train_model(file, m, optimizer, early_stopping=3, force_train=False):
model_path = models_path / (file + ".pt")
log_path = logs_path / (file + ".pickle")
if model_path.is_file() and log_path.is_file() and not force_train:
m = m.load_state_dict(torch.load(model_path, map_location=torch.device(device)))
logs = pickle.load(open(log_path, "rb"))
else:
m = m.to(device)
loss_fn = nn.CrossEntropyLoss()
stopping = EarlyStopping(early_stopping, model)
logs = []
for t in range(max_epochs):
print(f"Epoch {t+1}\n-------------------------------")
tacc, tloss = train(train_dataloader, m, loss_fn, optimizer)
vacc, vloss = test(val_dataloader, m, loss_fn)
logs.append((tacc, tloss, vacc, vloss))
stopping(m, vacc)
if stopping.early_stop:
break
m = stopping.best_model
torch.save(m.state_dict(), model_path)
pickle.dump(logs, open(log_path, "wb"))
stats = ["train_accuracy", "train_loss", "val_accuracy", "val_loss"]
d = pd.DataFrame(logs, columns=stats)
d.index += 1
return d
def display_result(d):
display(d.tail(5))
fig, axes = plt.subplots(1, 2, figsize=(10, 4), layout="constrained")
fig.suptitle("Learning curve")
ax = axes[0]
ax.set_title("Loss")
ax.plot(d.index, d.loc[:, "train_loss"], label="train", linestyle="dashed")
ax.plot(d.index, d.loc[:, "val_loss"], label="validation")
ax.set_xlabel("epoch")
ax.set_ylabel("loss")
ax.xaxis.set_major_locator(MaxNLocator(integer=True))
ax.legend()
ax = axes[1]
ax.set_title("Accuracy")
ax.plot(d.index, d.loc[:, "train_accuracy"], label="train", linestyle="dashed")
ax.plot(d.index, d.loc[:, "val_accuracy"], label="validation")
ax.set_xlabel("epoch")
ax.set_ylabel("accuracy")
ax.xaxis.set_major_locator(MaxNLocator(integer=True))
ax.legend()
plt.show()
Model suitability
Fully connected (dense) neural network models are very flexible and should perform relatively well on image data. However, we expect convolutional networks to perform significantly better. Compared to traditional models, neural networks are capable of modeling complicated functions, which on the one hand is desirable because it is certainly a complex function, however, it can also lead to overfitting or difficult training.
Base Network
This is our baseline fully connected neural network model.
class BaseNetwork(nn.Module):
def __init__(self):
super().__init__()
self.flatten = nn.Flatten()
self.linear_relu_stack = nn.Sequential(
nn.Linear(32 * 32, 512),
nn.ReLU(),
nn.Linear(512, 128),
nn.ReLU(),
nn.Linear(128, 128),
nn.ReLU(),
nn.Linear(128, 128),
nn.ReLU(),
nn.Linear(128, 10),
)
def forward(self, x):
x = self.flatten(x)
logits = self.linear_relu_stack(x)
return logits
model = BaseNetwork()
optimizer = torch.optim.Adam(model.parameters())
d_base = train_model("base", model, optimizer)
display_result(d_base)
| train_accuracy | train_loss | val_accuracy | val_loss | |
|---|---|---|---|---|
| 10 | 0.851 | 0.404 | 0.833 | 0.467 |
| 11 | 0.852 | 0.394 | 0.827 | 0.488 |
| 12 | 0.856 | 0.388 | 0.823 | 0.504 |
| 13 | 0.856 | 0.383 | 0.828 | 0.472 |
| 14 | 0.859 | 0.377 | 0.821 | 0.505 |
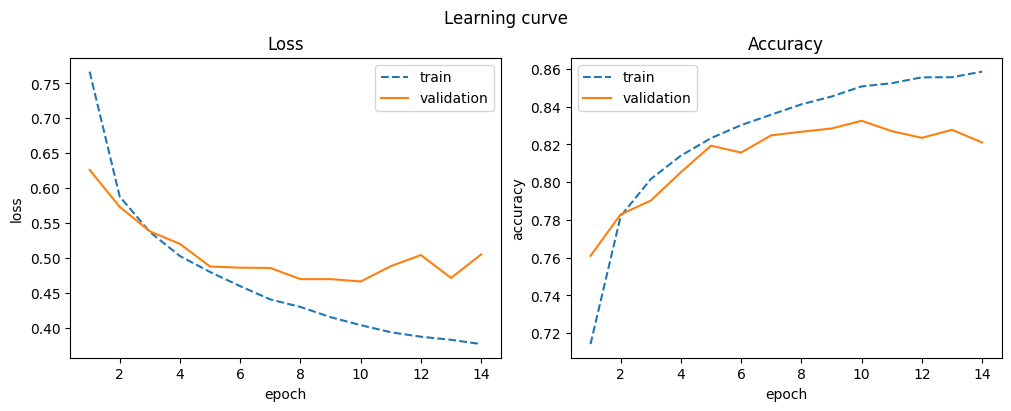
This base network serves as a reference for subsequent model modifications.
Wide Layers
We explore the impact of wider hidden layers.
class WideNetwork(nn.Module):
def __init__(self):
super().__init__()
self.flatten = nn.Flatten()
self.linear_relu_stack = nn.Sequential(
nn.Linear(32 * 32, 512),
nn.ReLU(),
nn.Linear(512, 512),
nn.ReLU(),
nn.Linear(512, 512),
nn.ReLU(),
nn.Linear(512, 256),
nn.ReLU(),
nn.Linear(256, 10),
)
def forward(self, x):
x = self.flatten(x)
logits = self.linear_relu_stack(x)
return logits
model = WideNetwork()
optimizer = torch.optim.Adam(model.parameters())
d_wide = train_model("wide", model, optimizer)
display_result(d_wide)
| train_accuracy | train_loss | val_accuracy | val_loss | |
|---|---|---|---|---|
| 12 | 0.853 | 0.396 | 0.839 | 0.478 |
| 13 | 0.855 | 0.386 | 0.833 | 0.470 |
| 14 | 0.858 | 0.378 | 0.836 | 0.475 |
| 15 | 0.861 | 0.371 | 0.835 | 0.495 |
| 16 | 0.864 | 0.365 | 0.837 | 0.495 |
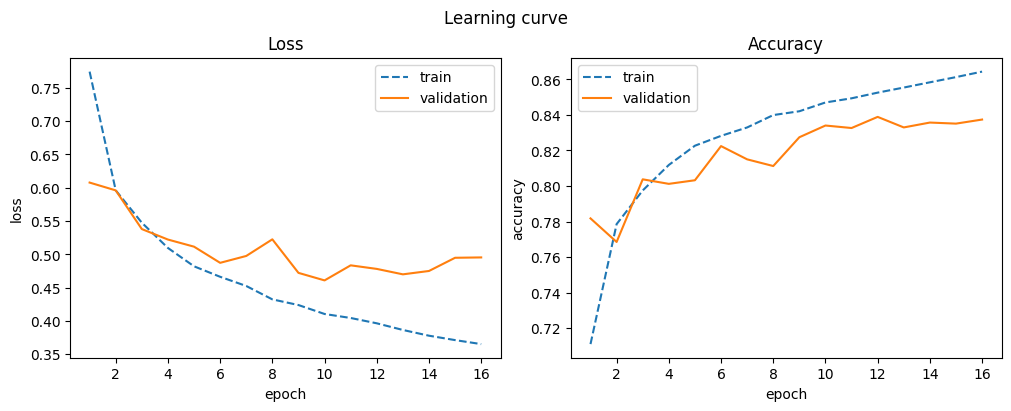
A slight improvement over the baseline is observed with wider layers.
Deep Network
Next, we evaluate a deeper network with more hidden layers.
class DeepNetwork(nn.Module):
def __init__(self):
super().__init__()
self.flatten = nn.Flatten()
self.linear_relu_stack = nn.Sequential(
nn.Linear(32 * 32, 512),
nn.ReLU(),
nn.Linear(512, 128),
nn.ReLU(),
nn.Linear(128, 128),
nn.ReLU(),
nn.Linear(128, 128),
nn.ReLU(),
nn.Linear(128, 128),
nn.ReLU(),
nn.Linear(128, 128),
nn.ReLU(),
nn.Linear(128, 128),
nn.ReLU(),
nn.Linear(128, 128),
nn.ReLU(),
nn.Linear(128, 10),
)
def forward(self, x):
x = self.flatten(x)
logits = self.linear_relu_stack(x)
return logits
model = DeepNetwork()
optimizer = torch.optim.Adam(model.parameters())
d_deep = train_model("deep", model, optimizer)
display_result(d_deep)
| train_accuracy | train_loss | val_accuracy | val_loss | |
|---|---|---|---|---|
| 26 | 0.883 | 0.313 | 0.849 | 0.467 |
| 27 | 0.884 | 0.311 | 0.851 | 0.466 |
| 28 | 0.883 | 0.314 | 0.853 | 0.468 |
| 29 | 0.888 | 0.303 | 0.849 | 0.476 |
| 30 | 0.887 | 0.302 | 0.846 | 0.474 |
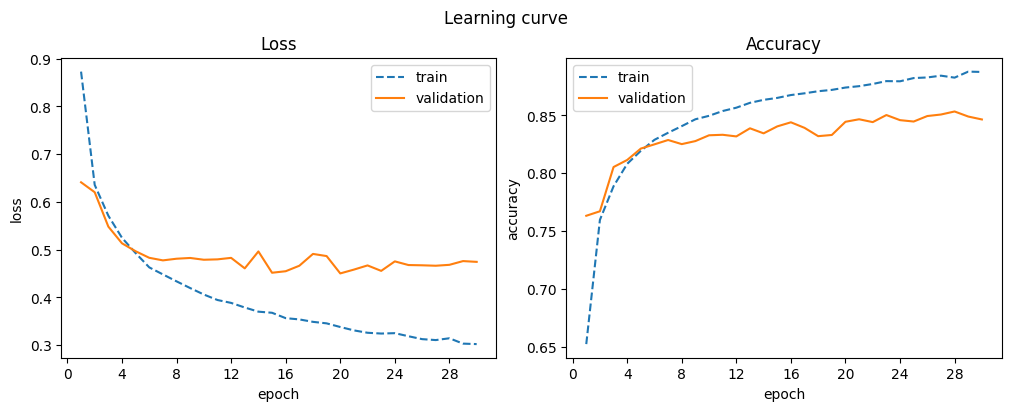
A deeper network shows significant improvement, though training time also increased.
SGD Optimizer
We test the Stochastic Gradient Descent (SGD) optimizer.
model = BaseNetwork()
optimizer = torch.optim.SGD(model.parameters())
d_sgd = train_model("sgd", model, optimizer)
display_result(d_sgd)
| train_accuracy | train_loss | val_accuracy | val_loss | |
|---|---|---|---|---|
| 26 | 0.874 | 0.346 | 0.839 | 0.442 |
| 27 | 0.876 | 0.341 | 0.840 | 0.438 |
| 28 | 0.878 | 0.337 | 0.841 | 0.438 |
| 29 | 0.879 | 0.332 | 0.842 | 0.437 |
| 30 | 0.881 | 0.328 | 0.843 | 0.436 |
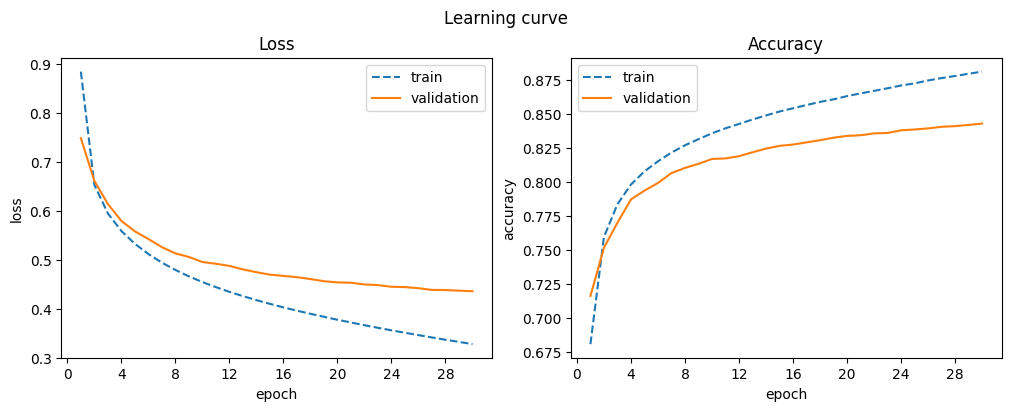
SGD offers more stable training, though it converges slower. Longer training might yield better results.
L2 Regularization
We apply L2 regularization to the base network.
model = BaseNetwork()
optimizer = torch.optim.Adam(model.parameters(), weight_decay=1e-2)
d_l2 = train_model("l2", model, optimizer)
display_result(d_l2)
| train_accuracy | train_loss | val_accuracy | val_loss | |
|---|---|---|---|---|
| 19 | 0.801 | 0.540 | 0.810 | 0.527 |
| 20 | 0.800 | 0.539 | 0.797 | 0.558 |
| 21 | 0.801 | 0.541 | 0.809 | 0.523 |
| 22 | 0.802 | 0.539 | 0.804 | 0.538 |
| 23 | 0.801 | 0.536 | 0.808 | 0.523 |
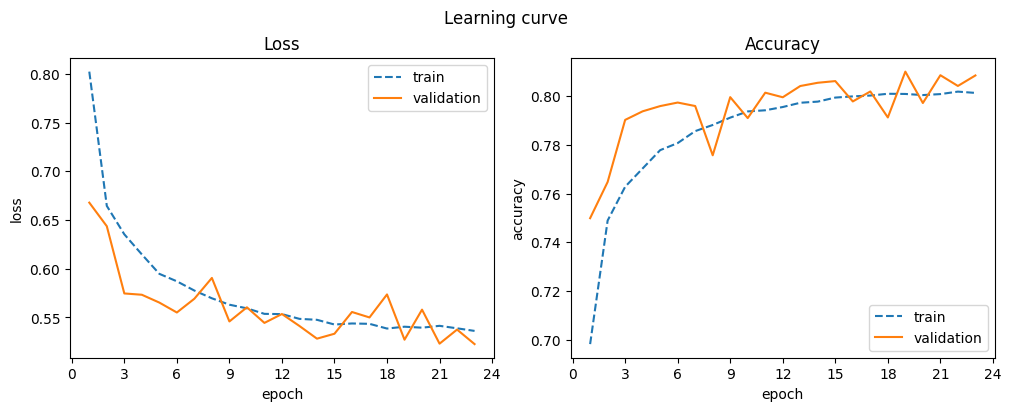
L2 regularization did not provide much benefit for this network. It might be more effective with larger models to prevent overfitting.
Batch Normalization
Batch normalization is introduced to improve training stability and performance.
class BatchNormNetwork(nn.Module):
def __init__(self):
super().__init__()
self.flatten = nn.Flatten()
self.linear_relu_stack = nn.Sequential(
nn.Linear(32 * 32, 512),
nn.BatchNorm1d(512),
nn.ReLU(),
nn.Linear(512, 128),
nn.BatchNorm1d(128),
nn.ReLU(),
nn.Linear(128, 128),
nn.BatchNorm1d(128),
nn.ReLU(),
nn.Linear(128, 128),
nn.BatchNorm1d(128),
nn.ReLU(),
nn.Linear(128, 10),
)
def forward(self, x):
x = self.flatten(x)
logits = self.linear_relu_stack(x)
return logits
model = BatchNormNetwork()
optimizer = torch.optim.Adam(model.parameters())
d_batch_norm = train_model("batch_norm", model, optimizer)
display_result(d_batch_norm)
| train_accuracy | train_loss | val_accuracy | val_loss | |
|---|---|---|---|---|
| 12 | 0.911 | 0.236 | 0.843 | 0.495 |
| 13 | 0.919 | 0.217 | 0.841 | 0.524 |
| 14 | 0.924 | 0.202 | 0.840 | 0.545 |
| 15 | 0.930 | 0.187 | 0.836 | 0.575 |
| 16 | 0.934 | 0.174 | 0.836 | 0.585 |
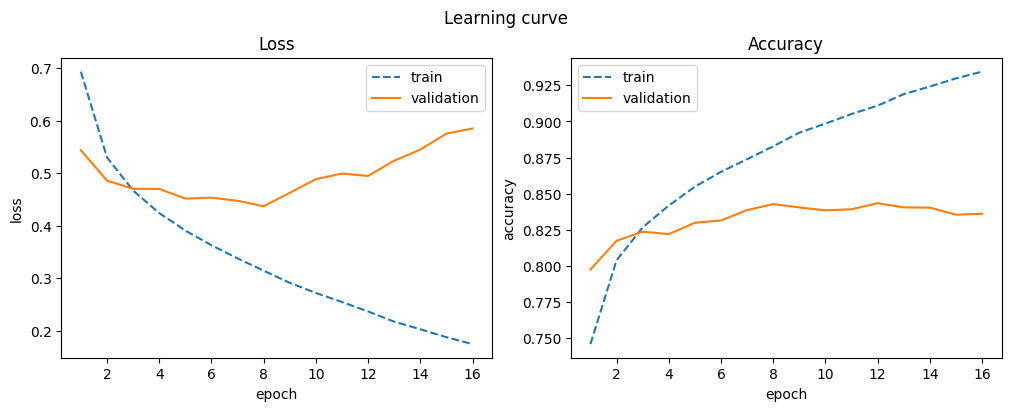
Batch normalization improves performance, but overfitting occurs with longer training, as indicated by the widening gap between training and validation curves.
Dropout
We incorporate dropout layers to mitigate overfitting.
class DropoutNetwork(nn.Module):
def __init__(self):
super().__init__()
self.flatten = nn.Flatten()
self.linear_relu_stack = nn.Sequential(
nn.Linear(32 * 32, 512),
nn.ReLU(),
nn.Dropout(0.5),
nn.Linear(512, 128),
nn.ReLU(),
nn.Dropout(0.4),
nn.Linear(128, 128),
nn.ReLU(),
nn.Dropout(0.3),
nn.Linear(128, 128),
nn.ReLU(),
nn.Dropout(0.2),
nn.Linear(128, 10),
)
def forward(self, x):
x = self.flatten(x)
logits = self.linear_relu_stack(x)
return logits
model = DropoutNetwork()
optimizer = torch.optim.Adam(model.parameters())
d_dropout = train_model("dropout", model, optimizer)
display_result(d_dropout)
| train_accuracy | train_loss | val_accuracy | val_loss | |
|---|---|---|---|---|
| 16 | 0.748 | 0.687 | 0.788 | 0.596 |
| 17 | 0.748 | 0.688 | 0.751 | 0.658 |
| 18 | 0.750 | 0.686 | 0.783 | 0.612 |
| 19 | 0.749 | 0.684 | 0.780 | 0.599 |
| 20 | 0.749 | 0.689 | 0.754 | 0.643 |
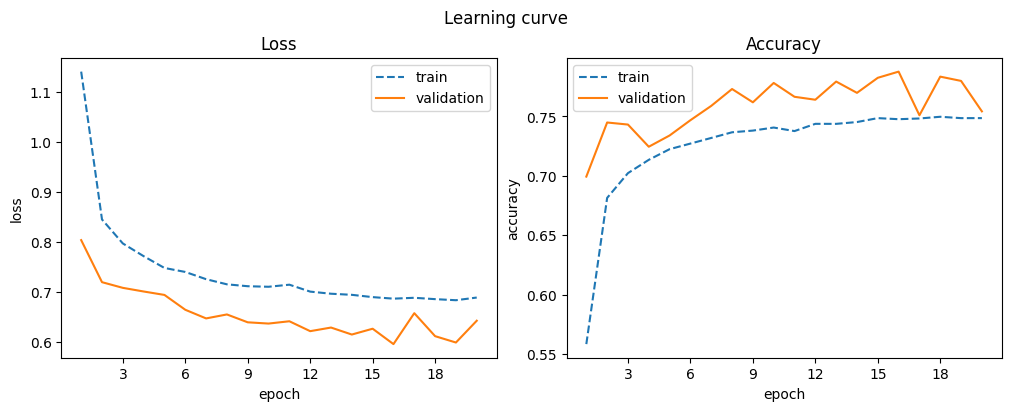
Dropout leads to a performance drop but is expected to improve generalization, especially in larger models. Validation accuracy is higher than training accuracy because dropout is disabled during evaluation.
Summary of Feedforward Networks
def display_summary(logs, labels):
accs = [l.loc[:, "val_accuracy"].max() for l in logs]
fig, ax = plt.subplots(figsize=(10, 6))
fig.suptitle("Comparison of networks")
for d, label in zip(logs, labels):
ax.plot(d.index, d.loc[:, "val_loss"], label=label, alpha=0.95)
ax.set_title("Learning curve")
ax.set_xlabel("epoch")
ax.set_ylabel("validation loss")
ax.legend()
plt.show()
fig, (ax1, ax2) = plt.subplots(2, 1, figsize=(10, 4))
fig.subplots_adjust(hspace=0.05)
for i, l in enumerate(labels):
ax1.bar(l, accs[i], alpha=0.7)
ax2.bar(l, accs[i], alpha=0.7)
ax1.set_ylim(0.75, 0.9)
ax2.set_ylim(0, 0.2)
ax1.spines.bottom.set_visible(False)
ax2.spines.top.set_visible(False)
ax1.set_xticks([])
ax2.set_yticks([0, 0.04, 0.10, 0.15])
ax1.xaxis.tick_top()
ax1.axhline(accs[0], alpha=0.4, c="black", linestyle="--", linewidth=0.51)
d = 0.5
kwargs = dict(
marker=[(-1, -d), (1, d)],
markersize=12,
linestyle="none",
color="k",
mec="k",
mew=1,
clip_on=False,
)
ax1.plot([0, 1], [0, 0], transform=ax1.transAxes, **kwargs)
ax2.plot([0, 1], [1, 1], transform=ax2.transAxes, **kwargs)
ax1.set_title("Best accuracy")
ax1.set_ylabel("validation accuracy")
plt.show()
display_summary(
[d_base, d_wide, d_deep, d_sgd, d_l2, d_batch_norm, d_dropout],
["base", "wide", "deep", "SGD", "L2", "batch norm", "dropout"],
)
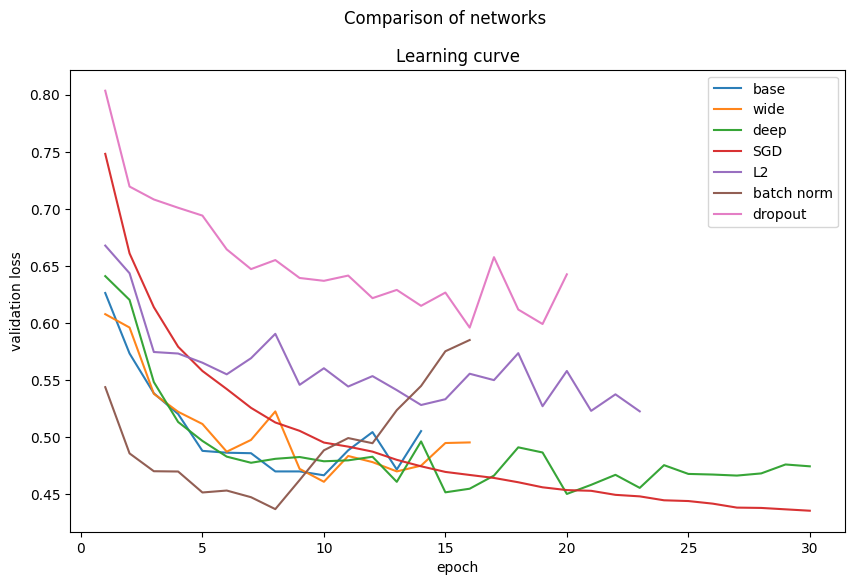
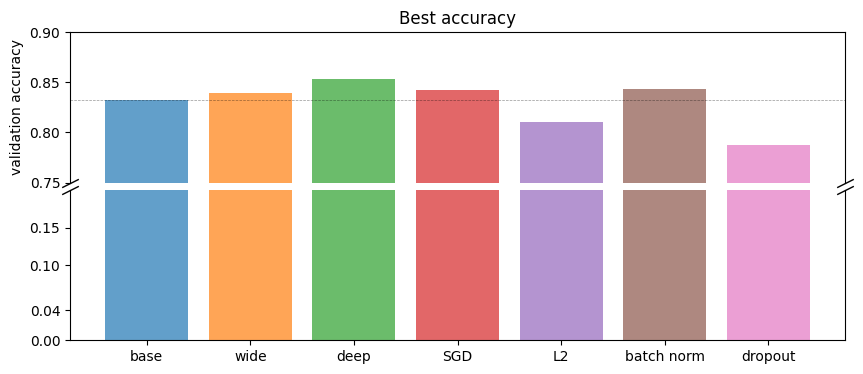
Deeper and wider networks outperform the baseline. SGD provides stable training. Batch normalization yields good results, while L2 and dropout did not improve performance on these smaller models.
Convolutional Neural Networks (CNNs)
CNNs are generally better for image data. We expect them to perform better than fully connected networks.
Base CNN
This is our baseline CNN model.
class CNN(nn.Module):
def __init__(self):
super().__init__()
self.conv1 = nn.Conv2d(1, 32, 3)
self.conv2 = nn.Conv2d(32, 64, 3)
self.pool = nn.MaxPool2d(2, 2)
self.fc1 = nn.Linear(2304, 64)
self.fc2 = nn.Linear(64, 10)
def forward(self, x):
x = self.pool(relu(self.conv1(x)))
x = self.pool(relu(self.conv2(x)))
x = torch.flatten(x, 1)
x = relu(self.fc1(x))
x = self.fc2(x)
return x
model = CNN()
optimizer = torch.optim.Adam(model.parameters())
d_base = train_model("base_cnn", model, optimizer)
display_result(d_base)
| train_accuracy | train_loss | val_accuracy | val_loss | |
|---|---|---|---|---|
| 8 | 0.911 | 0.234 | 0.875 | 0.381 |
| 9 | 0.917 | 0.222 | 0.868 | 0.414 |
| 10 | 0.921 | 0.210 | 0.867 | 0.432 |
| 11 | 0.924 | 0.199 | 0.870 | 0.435 |
| 12 | 0.926 | 0.196 | 0.872 | 0.436 |
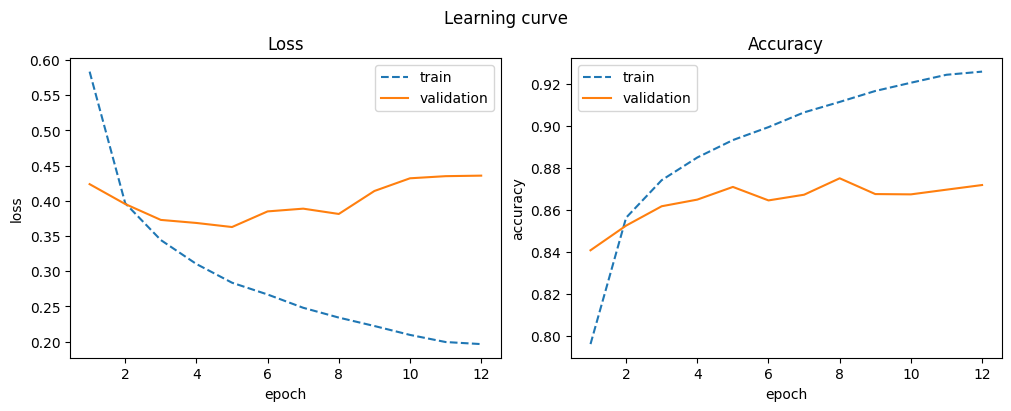
The base CNN already shows significant improvement over fully connected networks and converges quickly.
Wide CNN
class WideCNN(nn.Module):
def __init__(self):
super().__init__()
self.conv1 = nn.Conv2d(1, 32, 3)
self.conv2 = nn.Conv2d(32, 64, 3)
self.pool = nn.MaxPool2d(2, 2)
self.fc1 = nn.Linear(2304, 128)
self.fc2 = nn.Linear(128, 10)
def forward(self, x):
x = self.pool(relu(self.conv1(x)))
x = self.pool(relu(self.conv2(x)))
x = torch.flatten(x, 1)
x = relu(self.fc1(x))
x = self.fc2(x)
return x
model = WideCNN()
optimizer = torch.optim.Adam(model.parameters())
d_wide = train_model("wide_cnn", model, optimizer)
display_result(d_wide)
| train_accuracy | train_loss | val_accuracy | val_loss | |
|---|---|---|---|---|
| 4 | 0.880 | 0.321 | 0.862 | 0.380 |
| 5 | 0.889 | 0.295 | 0.853 | 0.410 |
| 6 | 0.898 | 0.272 | 0.849 | 0.448 |
| 7 | 0.904 | 0.256 | 0.854 | 0.444 |
| 8 | 0.911 | 0.238 | 0.857 | 0.444 |
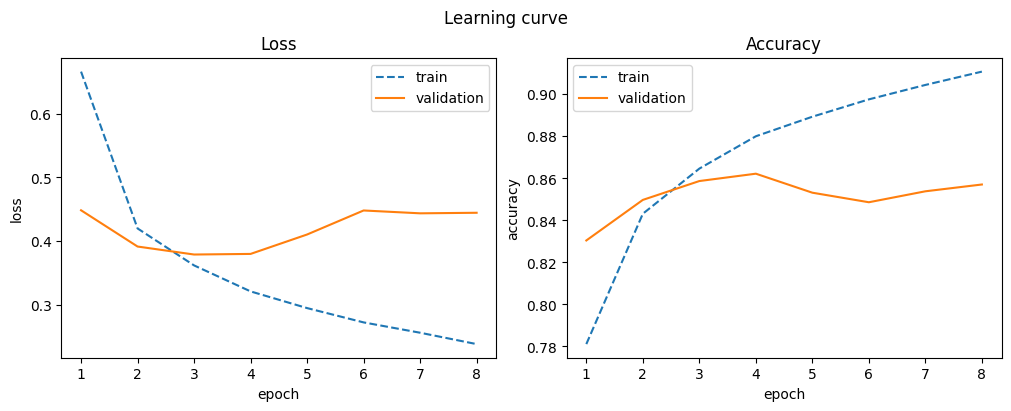
A wider CNN layer provides no improvement and still converges quickly.
Deep CNN
class DeepCNN(nn.Module):
def __init__(self):
super().__init__()
self.conv1 = nn.Conv2d(1, 64, 3)
self.conv2 = nn.Conv2d(64, 128, 3)
self.pool = nn.MaxPool2d(2, 2)
self.fc1 = nn.Linear(4608, 64)
self.fc2 = nn.Linear(64, 64)
self.fc3 = nn.Linear(64, 32)
self.fc4 = nn.Linear(32, 10)
def forward(self, x):
x = self.pool(relu(self.conv1(x)))
x = self.pool(relu(self.conv2(x)))
x = torch.flatten(x, 1)
x = relu(self.fc1(x))
x = relu(self.fc2(x))
x = relu(self.fc3(x))
x = self.fc4(x)
return x
model = DeepCNN()
optimizer = torch.optim.Adam(model.parameters())
d_deep = train_model("deep_cnn", model, optimizer)
display_result(d_deep)
| train_accuracy | train_loss | val_accuracy | val_loss | |
|---|---|---|---|---|
| 7 | 0.912 | 0.236 | 0.878 | 0.359 |
| 8 | 0.917 | 0.223 | 0.868 | 0.390 |
| 9 | 0.923 | 0.204 | 0.862 | 0.423 |
| 10 | 0.926 | 0.195 | 0.865 | 0.418 |
| 11 | 0.931 | 0.186 | 0.872 | 0.434 |
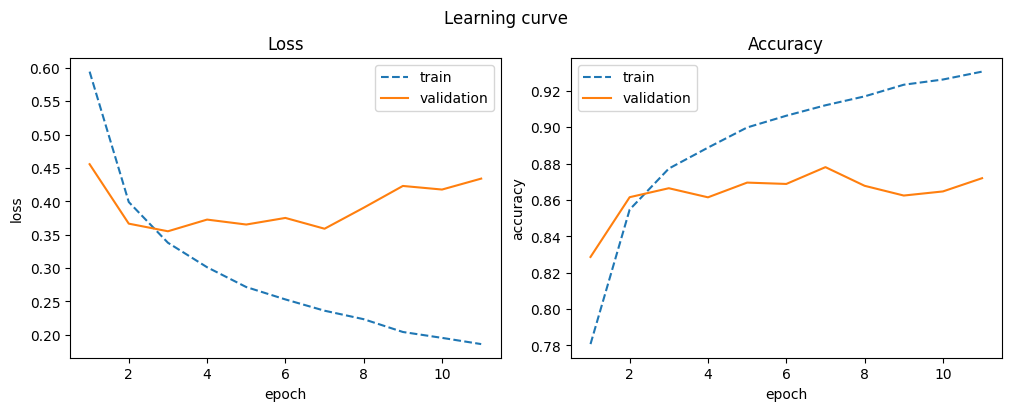
A deeper CNN offers minor improvement, but training becomes more volatile and shows signs of overfitting.
SGD Optimizer for CNN
model = CNN()
optimizer = torch.optim.SGD(model.parameters())
d_sgd = train_model("sgd_cnn", model, optimizer)
display_result(d_sgd)
| train_accuracy | train_loss | val_accuracy | val_loss | |
|---|---|---|---|---|
| 26 | 0.908 | 0.256 | 0.864 | 0.369 |
| 27 | 0.909 | 0.253 | 0.865 | 0.367 |
| 28 | 0.911 | 0.249 | 0.866 | 0.363 |
| 29 | 0.912 | 0.246 | 0.868 | 0.359 |
| 30 | 0.913 | 0.242 | 0.869 | 0.357 |
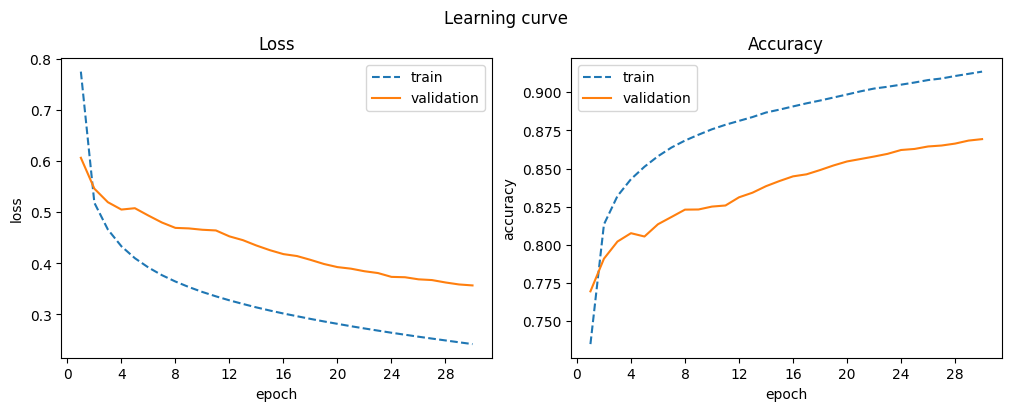
Similar to the fully connected networks, SGD offers stable but slower convergence for CNNs. Further training could be beneficial.
L2 Regularization for CNN
model = CNN()
optimizer = torch.optim.Adam(model.parameters(), weight_decay=1e-2)
d_l2 = train_model("l2_cnn", model, optimizer)
display_result(d_l2)
| train_accuracy | train_loss | val_accuracy | val_loss | |
|---|---|---|---|---|
| 12 | 0.874 | 0.343 | 0.869 | 0.346 |
| 13 | 0.875 | 0.343 | 0.860 | 0.370 |
| 14 | 0.876 | 0.340 | 0.868 | 0.353 |
| 15 | 0.876 | 0.339 | 0.869 | 0.350 |
| 16 | 0.877 | 0.336 | 0.868 | 0.349 |
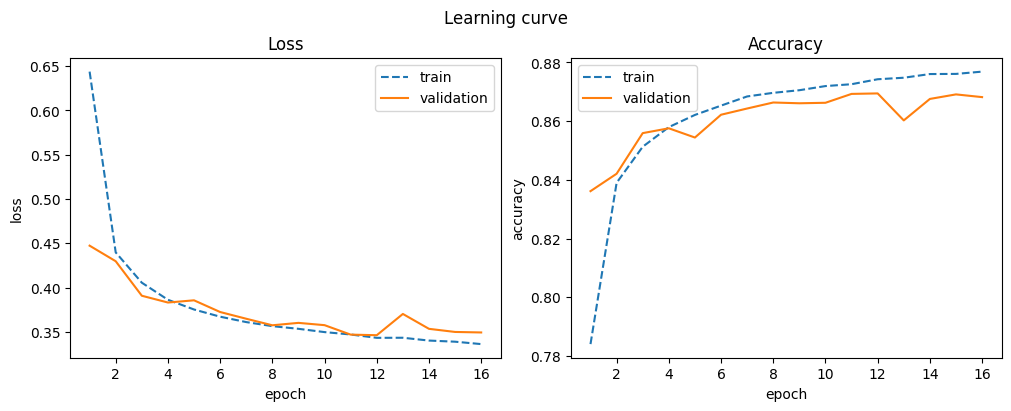
L2 regularization leads to more stable training for CNNs, even if it doesn’t always boost accuracy. This stability is crucial for larger models to generalize well.
Batch Normalization for CNN
class BatchNormCNN(nn.Module):
def __init__(self):
super().__init__()
self.conv1 = nn.Conv2d(1, 32, 3)
self.conv2 = nn.Conv2d(32, 64, 3)
self.conv1_bn = nn.BatchNorm2d(32)
self.conv2_bn = nn.BatchNorm2d(64)
self.pool = nn.MaxPool2d(2, 2)
self.fc1 = nn.Linear(2304, 64)
self.fc2 = nn.Linear(64, 10)
def forward(self, x):
x = self.pool(relu(self.conv1_bn(self.conv1(x))))
x = self.pool(relu(self.conv2_bn(self.conv2(x))))
x = torch.flatten(x, 1)
x = relu(self.fc1(x))
x = self.fc2(x)
return x
model = BatchNormCNN()
optimizer = torch.optim.Adam(model.parameters())
d_batch_norm = train_model("batch_norm_cnn", model, optimizer)
display_result(d_batch_norm)
| train_accuracy | train_loss | val_accuracy | val_loss | |
|---|---|---|---|---|
| 9 | 0.925 | 0.203 | 0.881 | 0.337 |
| 10 | 0.931 | 0.188 | 0.877 | 0.368 |
| 11 | 0.935 | 0.176 | 0.880 | 0.376 |
| 12 | 0.940 | 0.163 | 0.881 | 0.386 |
| 13 | 0.945 | 0.151 | 0.879 | 0.399 |
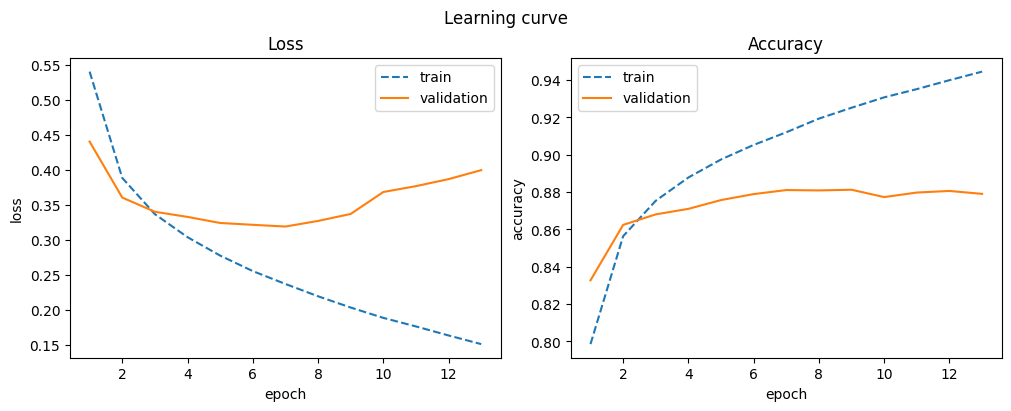
Batch normalization for CNNs results in a smoother training curve and a slight accuracy boost.
Dropout for CNN
class DropoutCNN(nn.Module):
def __init__(self):
super().__init__()
self.conv1 = nn.Conv2d(1, 32, 3)
self.conv2 = nn.Conv2d(32, 64, 3)
self.dropout = nn.Dropout2d(0.5)
self.pool = nn.MaxPool2d(2, 2)
self.fc1 = nn.Linear(2304, 64)
self.fc2 = nn.Linear(64, 10)
def forward(self, x):
x = self.pool(self.dropout(relu(self.conv1(x))))
x = self.pool(self.dropout(relu(self.conv2(x))))
x = torch.flatten(x, 1)
x = relu(self.fc1(x))
x = self.fc2(x)
return x
model = DropoutCNN()
optimizer = torch.optim.Adam(model.parameters())
d_dropout = train_model("dropout_cnn", model, optimizer)
display_result(d_dropout)
| train_accuracy | train_loss | val_accuracy | val_loss | |
|---|---|---|---|---|
| 21 | 0.858 | 0.379 | 0.874 | 0.332 |
| 22 | 0.861 | 0.375 | 0.865 | 0.350 |
| 23 | 0.860 | 0.376 | 0.872 | 0.338 |
| 24 | 0.861 | 0.373 | 0.871 | 0.332 |
| 25 | 0.862 | 0.373 | 0.870 | 0.341 |
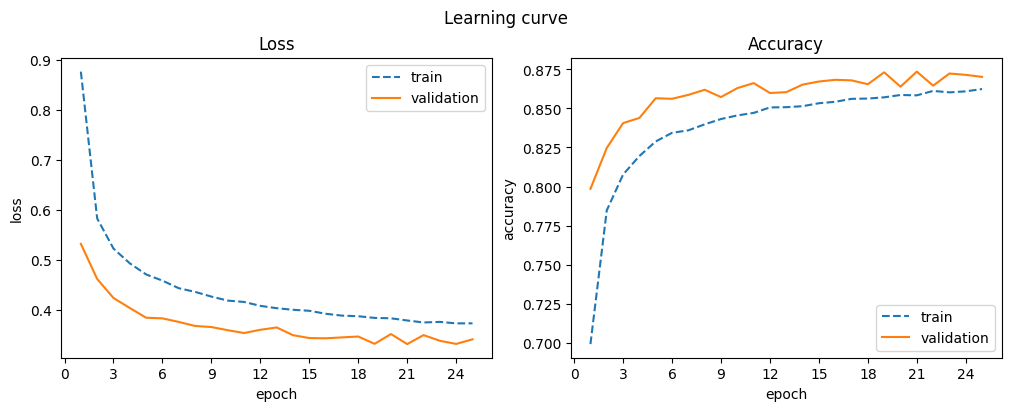
Dropout works better with CNNs than with fully connected networks. It helps prevent overfitting, leading to better generalization.
Summary of CNNs
display_summary(
[d_base, d_wide, d_deep, d_sgd, d_l2, d_batch_norm, d_dropout],
["base", "wide", "deep", "SGD", "L2", "batch norm", "dropout"],
)
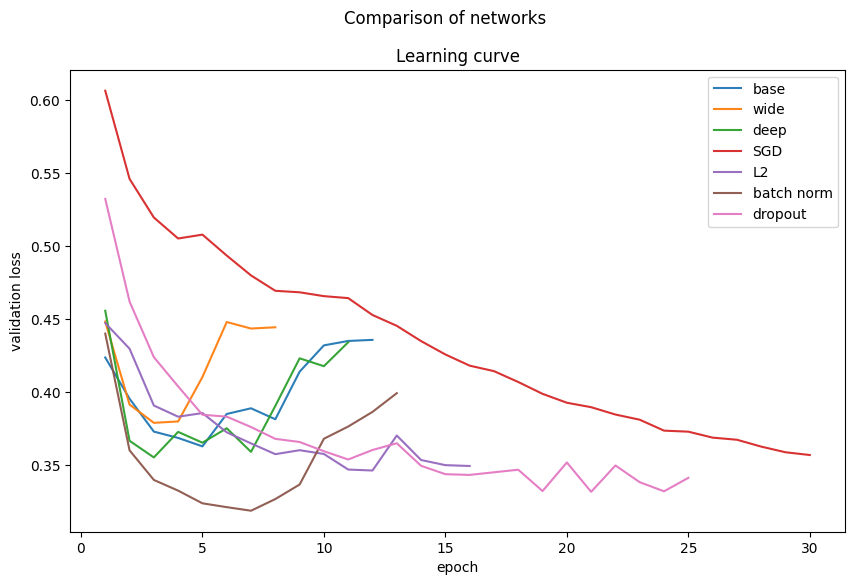
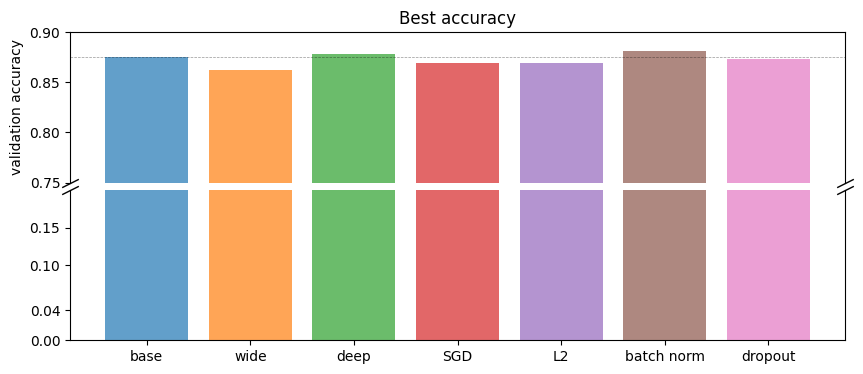
CNNs generally outperform fully connected networks on image data. Batch normalization and deeper networks show improved performance. Regularization techniques like L2 and dropout help stabilize training and improve generalization.
Final Model
Our final model combines successful elements from previous experiments: a deep and wide CNN architecture with batch normalization, dropout, and L2 regularization. We will train it using Adam initially, then fine-tune with SGD for optimal accuracy and stability.
class FinalCNNet(nn.Module):
def __init__(self):
super().__init__()
self.pool = nn.MaxPool2d(2, 2)
self.conv1 = nn.Conv2d(1, 64, 2)
self.conv1_bn = nn.BatchNorm2d(64)
self.conv1_do = nn.Dropout2d(0.1)
self.conv2 = nn.Conv2d(64, 128, 2)
self.conv2_bn = nn.BatchNorm2d(128)
self.conv2_do = nn.Dropout2d(0.3)
self.conv3 = nn.Conv2d(128, 256, 2)
self.conv3_bn = nn.BatchNorm2d(256)
self.conv3_do = nn.Dropout2d(0.5)
self.conv4 = nn.Conv2d(256, 512, 4)
self.conv4_bn = nn.BatchNorm2d(512)
self.conv4_do = nn.Dropout2d(0.5)
self.fc1 = nn.Linear(4608, 512)
self.fc1_bn = nn.BatchNorm1d(512)
self.fc1_do = nn.Dropout(0.1)
self.fc2 = nn.Linear(512, 256)
self.fc2_bn = nn.BatchNorm1d(256)
self.fc2_do = nn.Dropout(0.3)
self.fc3 = nn.Linear(256, 128)
self.fc3_bn = nn.BatchNorm1d(128)
self.fc3_do = nn.Dropout(0.5)
self.fc4 = nn.Linear(128, 64)
self.fc4_bn = nn.BatchNorm1d(64)
self.fc4_do = nn.Dropout(0.5)
self.fc5 = nn.Linear(64, 10)
def forward(self, x):
x = self.pool(self.conv1_do(relu(self.conv1_bn(self.conv1(x)))))
x = self.pool(self.conv2_do(relu(self.conv2_bn(self.conv2(x)))))
x = self.conv3_do(relu(self.conv3_bn(self.conv3(x))))
x = self.conv4_do(relu(self.conv4_bn(self.conv4(x))))
x = torch.flatten(x, 1)
x = self.fc1_do(relu(self.fc1_bn(self.fc1(x))))
x = self.fc2_do(relu(self.fc2_bn(self.fc2(x))))
x = self.fc3_do(relu(self.fc3_bn(self.fc3(x))))
x = self.fc4_do(relu(self.fc4_bn(self.fc4(x))))
x = self.fc5(x)
return x
RETRAIN = False
max_epochs = 200
model = FinalCNNet()
optimizer0 = torch.optim.Adam(model.parameters(), weight_decay=1e-3)
optimizer1 = torch.optim.SGD(model.parameters(), weight_decay=1e-3)
optimizer2 = torch.optim.SGD(model.parameters())
d_final0 = train_model("final0", model, optimizer0, 4, RETRAIN)
d_final1 = train_model("final1", model, optimizer1, 4, RETRAIN)
d_final2 = train_model("final2", model, optimizer2, 4, RETRAIN)
display_result(pd.concat((d_final0, d_final1, d_final2)).reset_index())
| index | train_accuracy | train_loss | val_accuracy | val_loss | |
|---|---|---|---|---|---|
| 149 | 39 | 0.909 | 0.282 | 0.914 | 0.246 |
| 150 | 40 | 0.908 | 0.283 | 0.914 | 0.246 |
| 151 | 41 | 0.909 | 0.281 | 0.914 | 0.246 |
| 152 | 42 | 0.908 | 0.284 | 0.914 | 0.246 |
| 153 | 43 | 0.910 | 0.281 | 0.914 | 0.246 |
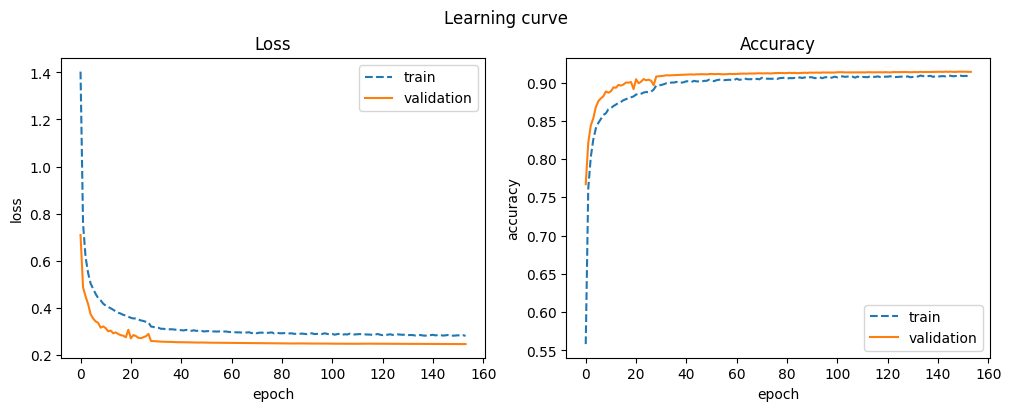
Evaluation
We now evaluate the final model’s performance on the test data.
final = load_model("final2", FinalCNNet()).to(device)
y_test_proba_pred_path = outputs_path / "y_test_proba_pred.pickle"
y_test_proba_hat = predict_proba(test_dataloader, final, y_test_proba_pred_path)
y_test_hat = np.argmax(y_test_proba_hat, axis=1)
acc = np.round(accuracy_score(y_test, y_test_hat), 3)
print(f"Test accuracy: {acc}")
Test accuracy: 0.916
The model achieved a test accuracy of 91.6%.
report = pd.DataFrame(
classification_report(y_test, y_test_hat, target_names=cats, output_dict=True)
).T
display(report)
| precision | recall | f1-score | support | |
|---|---|---|---|---|
| T-shirt/top | 0.858 | 0.887 | 0.872 | 1115.000 |
| Trouser | 0.995 | 0.994 | 0.995 | 1101.000 |
| Pullover | 0.882 | 0.871 | 0.877 | 1047.000 |
| Dress | 0.892 | 0.911 | 0.901 | 1028.000 |
| Coat | 0.861 | 0.867 | 0.864 | 1061.000 |
| Sandal | 0.989 | 0.967 | 0.978 | 1024.000 |
| Shirt | 0.771 | 0.743 | 0.756 | 1058.000 |
| Sneaker | 0.951 | 0.977 | 0.964 | 998.000 |
| Bag | 0.991 | 0.977 | 0.984 | 1044.000 |
| Ankle boot | 0.978 | 0.974 | 0.976 | 1024.000 |
| accuracy | 0.916 | 0.916 | 0.916 | 0.916 |
| macro avg | 0.917 | 0.917 | 0.917 | 10500.000 |
| weighted avg | 0.916 | 0.916 | 0.916 | 10500.000 |
def display_confusion_matrix(ax, norm=None):
ConfusionMatrixDisplay.from_predictions(
VEC_IL(y_test),
VEC_IL(y_test_hat),
labels=cats,
normalize=norm,
xticks_rotation="vertical",
colorbar=False,
cmap="Blues",
ax=ax,
)
ax.set_title("Confusion matrix (final model, test data)")
ax.set_xlabel("Predicted class")
ax.set_ylabel("True class", size=16)
ax.tick_params(axis="both", which="major")
ax.grid(False)
fig, ax = plt.subplots(1, 1, figsize=(8, 8), layout="constrained")
display_confusion_matrix(ax)
plt.show()
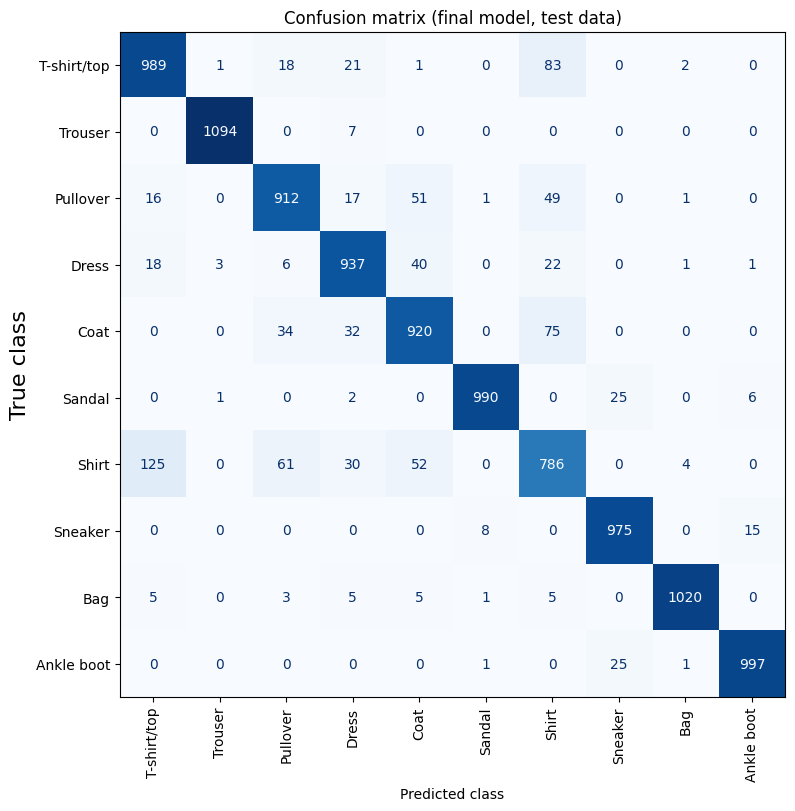
The model frequently confuses “Shirt” with “T-shirt/top,” and also struggles with “Coat/Shirt” and “Pullover/Shirt” distinctions.
fig, axes = plt.subplots(4, 3, figsize=(10, 10), layout="constrained")
fig.suptitle("ROC and AUC")
fig.supxlabel("True positive rate")
fig.supylabel("False positive rate")
for i, (cat, ax) in enumerate(zip(cats, fig.axes[:10])):
disp = RocCurveDisplay.from_predictions(
y_test == i, y_test_proba_hat[:, i], ax=ax, name=f"{cat} v rest"
)
ax.set(xlabel=None, ylabel=None)
for ax in fig.axes[10:]:
ax.remove()
plt.show()
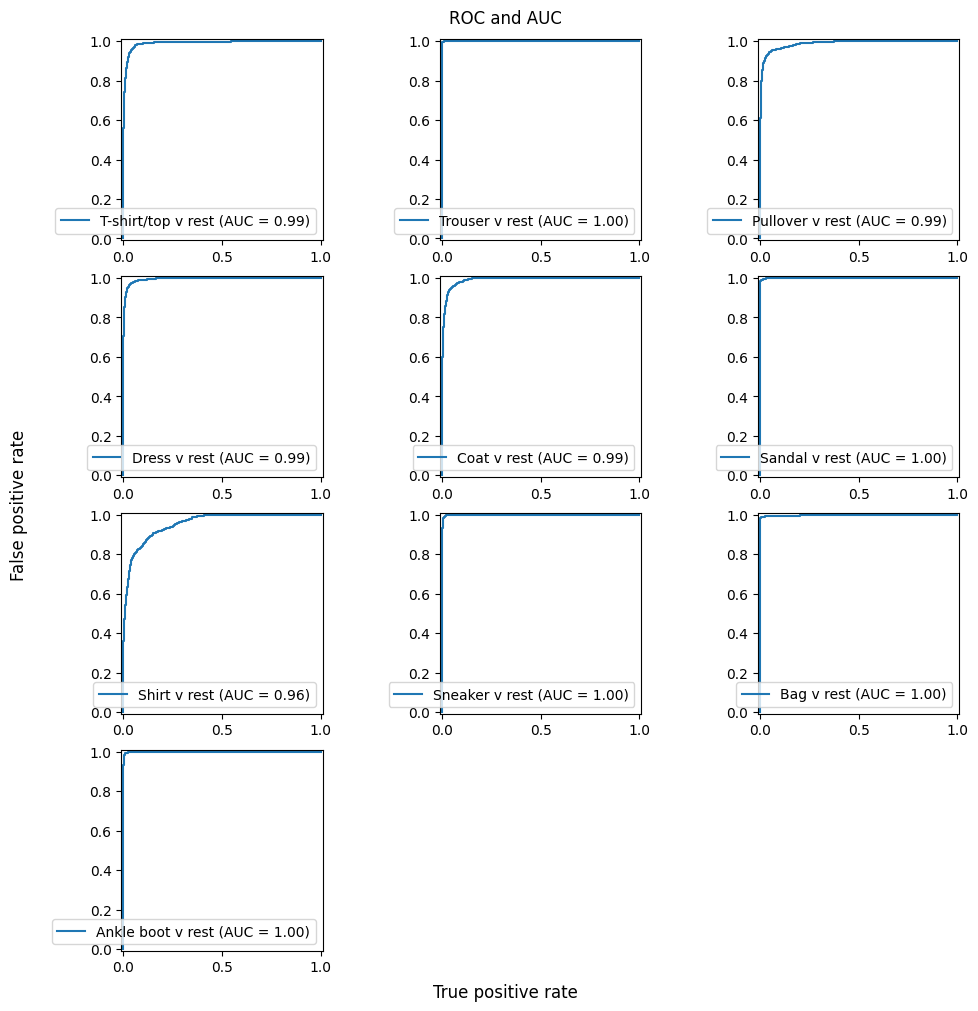
The model performs exceptionally well for “Trouser”, “Ankle boot”, “Bag”, “Sneaker”, and “Sandal” classes (AUC = 1). However, it struggles with “Shirt”, “Coat”, “Pullover”, and “T-shirt/top”.
Sample Predictions
edf = pd.read_csv(eval_file)
id = edf.loc[:, "ID"]
X_eval = edf.drop("ID", axis=1).to_numpy()
eval_dataloader = DataLoader(
TensorDataset(torch.Tensor(X_eval).reshape((-1, 1, 32, 32))),
batch_size=batch_size,
)
eval_pred_path = outputs_path / "eval_pred.pickle"
final = load_model("final2", FinalCNNet()).to(device)
y_eval = predict(eval_dataloader, final, eval_pred_path)
d = pd.DataFrame()
d["ID"] = id
d["label"] = y_eval
d.to_csv(res_file, index=False)
fig, ax = plt.subplots(4, 8, figsize=(10, 6))
fig.suptitle("Sample from evaluation.csv (inverted brightness)")
for j in range(4):
for i in range(8):
ax[j, i].imshow(X_eval[5 * j + i].reshape((32, 32)), cmap="Greys")
ax[j, i].set_title(MAP_IL[d.loc[5 * j + i, "label"]], fontsize=9)
ax[j, i].set_axis_off()
plt.show()

The first 32 predictions appear reasonable. Let’s visualize predictions by category.
for c in range(10):
fig, axes = plt.subplots(2, 10, figsize=(10, 2))
fig.suptitle(f"{MAP_IL[c]}")
d = X_eval[y_eval == c]
for i in range(10):
axes[0][i].imshow(d[i].reshape((32, 32)), cmap="Greys")
axes[0][i].set_axis_off()
axes[1][i].imshow(d[i + 10].reshape((32, 32)), cmap="Greys")
axes[1][i].set_axis_off()
plt.show()