This project analyzes the ex1221 dataset from the Sleuth2 R package to explore the factors influencing nitrate concentration (NO3) in river mouths.
# Load required packages
library(Sleuth2)
library(ggplot2)
library(GGally)
library(cowplot)
library(lmtest)
# Suppress package startup messages if needed
Sys.setenv(`_R_S3_METHOD_REGISTRATION_NOTE_OVERWRITES_` = "false")
suppressPackageStartupMessages(library(zoo))
Task 1: Data Exploration
Load the dataset and perform basic statistical investigations:
- Briefly describe the data and individual variables.
- Determine the most important statistical measures that best characterize the data.
- Represent the data appropriately using selected graphs.
attach(ex1221)
df <- ex1221
ex1221
| River | Country | Discharge | Runoff | Area | Density | NO3 | Export | Dep | NPrec | Prec | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| <chr> | <fct> | <dbl> | <dbl> | <dbl> | <dbl> | <dbl> | <dbl> | <dbl> | <dbl> | <dbl> | |
| 1 | Adige | Italy | 223.00 | 18.3 | 1220 | 102.00 | 67.0 | 1224.7 | 1237.5 | 46.0 | 84.8 |
| 2 | Amazon | S_America | 175000.00 | 24.8 | 7050000 | 1.00 | 3.0 | 74.5 | 120.6 | 2.1 | 181.1 |
| 3 | Caragh | Ireland | 7.29 | 45.6 | 160 | 7.15 | 3.6 | 164.0 | 86.5 | 2.6 | 104.9 |
| 4 | Columbia | USA | 7900.00 | 11.8 | 670000 | 10.00 | 26.6 | 313.6 | 62.8 | 2.0 | 99.1 |
| 5 | Danube | Rumania | 6500.00 | 8.1 | 805000 | 90.00 | 46.0 | 371.4 | 826.4 | 45.0 | 57.9 |
| 6 | Delaware | USA | 336.00 | 19.1 | 17600 | 100.00 | 61.0 | 1167.2 | 851.7 | 25.0 | 107.4 |
| 7 | Fraser | Canada | 3550.00 | 16.1 | 220000 | 2.00 | 6.4 | 103.3 | 739.7 | 16.0 | 145.8 |
| 8 | Ganges | India | 16000.00 | 14.9 | 1070000 | 300.00 | 91.3 | 1361.4 | 294.3 | 5.8 | 160.0 |
| 9 | Glaama | Norway | 706.00 | 16.9 | 41770 | 12.00 | 24.0 | 405.7 | 975.0 | 45.0 | 68.3 |
| 10 | Huanghe | China | 1470.00 | 2.0 | 750000 | 200.00 | 139.0 | 272.6 | 286.4 | 28.0 | 32.3 |
| 11 | Hudson | USA | 560.00 | 16.1 | 34700 | 150.00 | 47.8 | 771.4 | 851.7 | 25.0 | 107.4 |
| 12 | Kazan_and_Back | Canada | 1900.00 | 6.1 | 312000 | 0.40 | 1.1 | 6.7 | 60.9 | 7.0 | 27.4 |
| 13 | Mackenzie | Canada | 10600.00 | 5.9 | 1787000 | 0.15 | 5.7 | 33.8 | 73.9 | 7.0 | 33.3 |
| 14 | Magdalena | Columbia | 7500.00 | 31.3 | 240000 | 30.00 | 17.0 | 531.3 | 87.5 | 2.6 | 106.2 |
| 15 | Mekong | SE_Asia | 15000.00 | 19.2 | 783000 | 43.00 | 17.0 | 325.7 | 334.1 | 7.6 | 139.2 |
| 16 | Mersey | England | 21.00 | 17.5 | 1200 | 200.00 | 156.0 | 2730.0 | 919.4 | 28.9 | 100.3 |
| 17 | Meuse | Nthlnds/Belgium | 317.00 | 9.1 | 34900 | 250.00 | 230.0 | 2089.1 | 742.3 | 36.0 | 65.0 |
| 18 | Mississippi | USA | 16100.00 | 5.0 | 3220000 | 30.00 | 63.0 | 315.0 | 691.7 | 19.0 | 114.8 |
| 19 | Murray-Darling | Australia | 318.20 | 0.3 | 1073000 | 1.50 | 15.0 | 4.4 | 74.8 | 4.4 | 53.6 |
| 20 | Nelson | Canada | 2370.00 | 2.2 | 1070000 | 2.00 | 5.0 | 11.1 | 248.6 | 21.0 | 37.3 |
| 21 | Niger | W_Africa | 7000.00 | 6.2 | 1125000 | 20.00 | 7.0 | 43.6 | 555.2 | 9.6 | 181.6 |
| 22 | Nile | NE_Africa | 950.00 | 0.3 | 2960000 | 50.00 | 20.0 | 6.4 | 50.9 | 10.2 | 15.7 |
| 23 | Orange | S_Africa | 170.00 | 0.2 | 1020000 | 20.00 | 50.0 | 8.3 | 154.9 | 23.0 | 18.1 |
| 24 | Orinoco | Venezuela | 33900.00 | 33.9 | 1000000 | 2.00 | 6.0 | 203.4 | 92.5 | 3.0 | 97.3 |
| 25 | Parana | Argentina | 15900.00 | 5.7 | 2800000 | 10.00 | 14.2 | 80.6 | 216.2 | 9.9 | 75.8 |
| 26 | Po | Italy | 1470.00 | 22.0 | 66700 | 232.00 | 102.0 | 2247.3 | 1237.5 | 46.0 | 84.8 |
| 27 | Rhine | Europe | 2200.00 | 11.9 | 185300 | 300.00 | 286.0 | 3395.6 | 1647.9 | 60.0 | 86.6 |
| 28 | Rhone | France | 1700.00 | 17.7 | 96000 | 100.00 | 57.2 | 1012.9 | 695.9 | 30.0 | 73.2 |
| 29 | Shannon | Ireland | 190.00 | 13.5 | 14000 | 35.00 | 54.0 | 727.7 | 252.8 | 8.6 | 92.7 |
| 30 | Stikine | Canada/USA | 1100.00 | 22.0 | 50000 | 1.00 | 6.1 | 134.2 | 76.8 | 1.0 | 242.1 |
| 31 | St._Lawrence | Canada/USA | 10700.00 | 10.4 | 1025000 | 15.00 | 16.0 | 167.0 | 673.2 | 21.0 | 101.1 |
| 32 | Susquehanna | USA | 1100.00 | 15.1 | 73000 | 100.00 | 66.0 | 994.5 | 821.5 | 25.0 | 103.6 |
| 33 | Tees | England | 50.00 | 27.7 | 1806 | 100.00 | 75.0 | 2076.5 | 608.7 | 33.0 | 58.2 |
| 34 | Thames | England | 78.00 | 7.8 | 9950 | 400.00 | 520.0 | 4076.4 | 1125.1 | 61.0 | 58.2 |
| 35 | Tiber | Italy | 230.00 | 13.5 | 17000 | 262.00 | 100.0 | 1352.9 | 1237.5 | 46.0 | 84.8 |
| 36 | Uruguay | S_America | 3850.00 | 10.5 | 365000 | 10.00 | 29.0 | 305.9 | 355.6 | 13.7 | 86.1 |
| 37 | Vistula | Poland | 1100.00 | 5.5 | 200000 | 120.00 | 70.5 | 387.8 | 832.8 | 47.0 | 55.9 |
| 38 | Volga | Russia | 8200.00 | 6.1 | 1350000 | 50.00 | 30.0 | 182.2 | 151.8 | 13.0 | 36.8 |
| 39 | Yangtze | China | 29000.00 | 15.4 | 1900000 | 200.00 | 58.2 | 897.0 | 370.5 | 10.0 | 116.8 |
| 40 | Yukon | Canada | 6180.00 | 7.4 | 831000 | 0.40 | 9.3 | 69.2 | 185.4 | 7.8 | 78.5 |
| 41 | Zaire | Zaire | 39730.00 | 10.4 | 3820000 | 11.70 | 6.0 | 62.4 | 467.2 | 10.0 | 147.3 |
| 42 | Zambezi | SE_Africa | 3200.00 | 2.5 | 1300000 | 15.00 | 9.3 | 22.9 | 138.5 | 8.4 | 51.8 |
Data Description
Rising nitrate levels in river mouths cause an increase in algae in coastal waters. Therefore, data was collected to investigate the relationship between nitrate concentration in rivers and human population density. We have the following variables available:
| Variable | Description | Units |
|---|---|---|
| River | River name | |
| Country | Territory through which the river flows | |
| Discharge | Average annual river discharge into the ocean | m³/sec |
| Runoff | Average annual specific runoff from the watershed | liter/(sec x km²) |
| Area | Area of the watershed | km² |
| Export | Nitrate export (product of Discharge and NO3) | |
| Dep | Deposition (proportional to the product of NPrec and Prec) | |
| NPrec | Precipitation - nitrate concentration | micromol NO3/(sec × km²)) |
| Prec | Precipitation | cm/year |
| Density | Population density | people/km² |
| NO3 | Nitrate concentration | micromol NO3/liter |
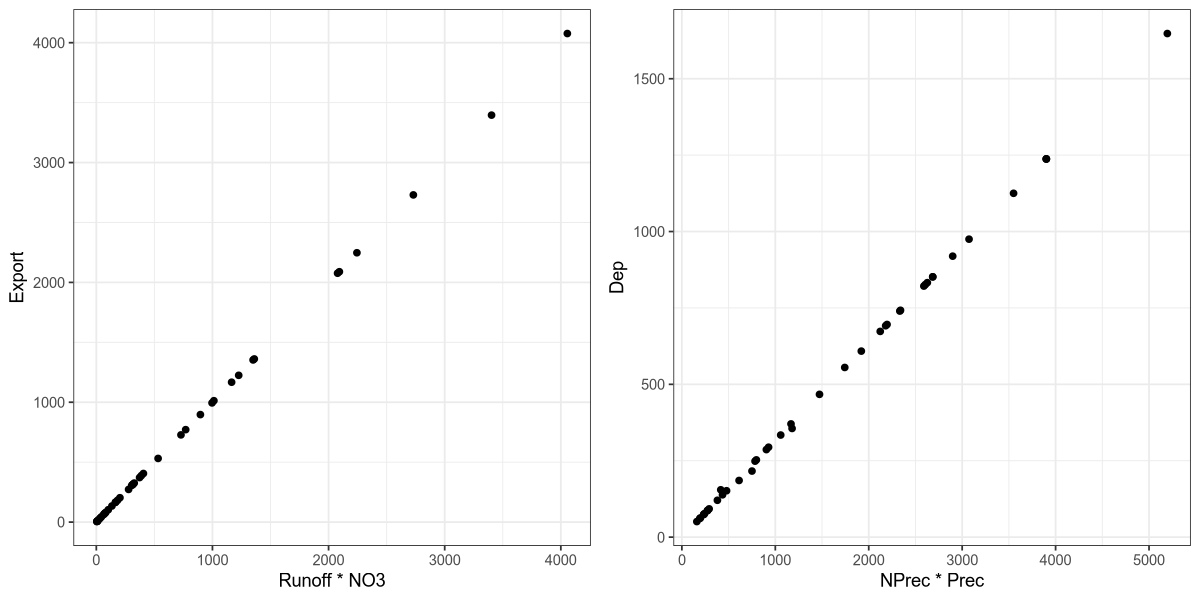
In the dataset, we observe the artificial variables Export and Dep, which were calculated from other measured values:
options(repr.plot.width = 10)
options(repr.plot.height = 5)
p1 <- ggplot(df, aes(x = Runoff * NO3, y = Export)) +
geom_point() + theme_bw()
p2 <- ggplot(df, aes(x = NPrec * Prec, y = Dep)) +
geom_point() + theme_bw()
plot_grid(p1, p2, ncol = 2)
Statistical Measures
Nitrate Concentration
options(repr.plot.width = 10)
options(repr.plot.height = 8)
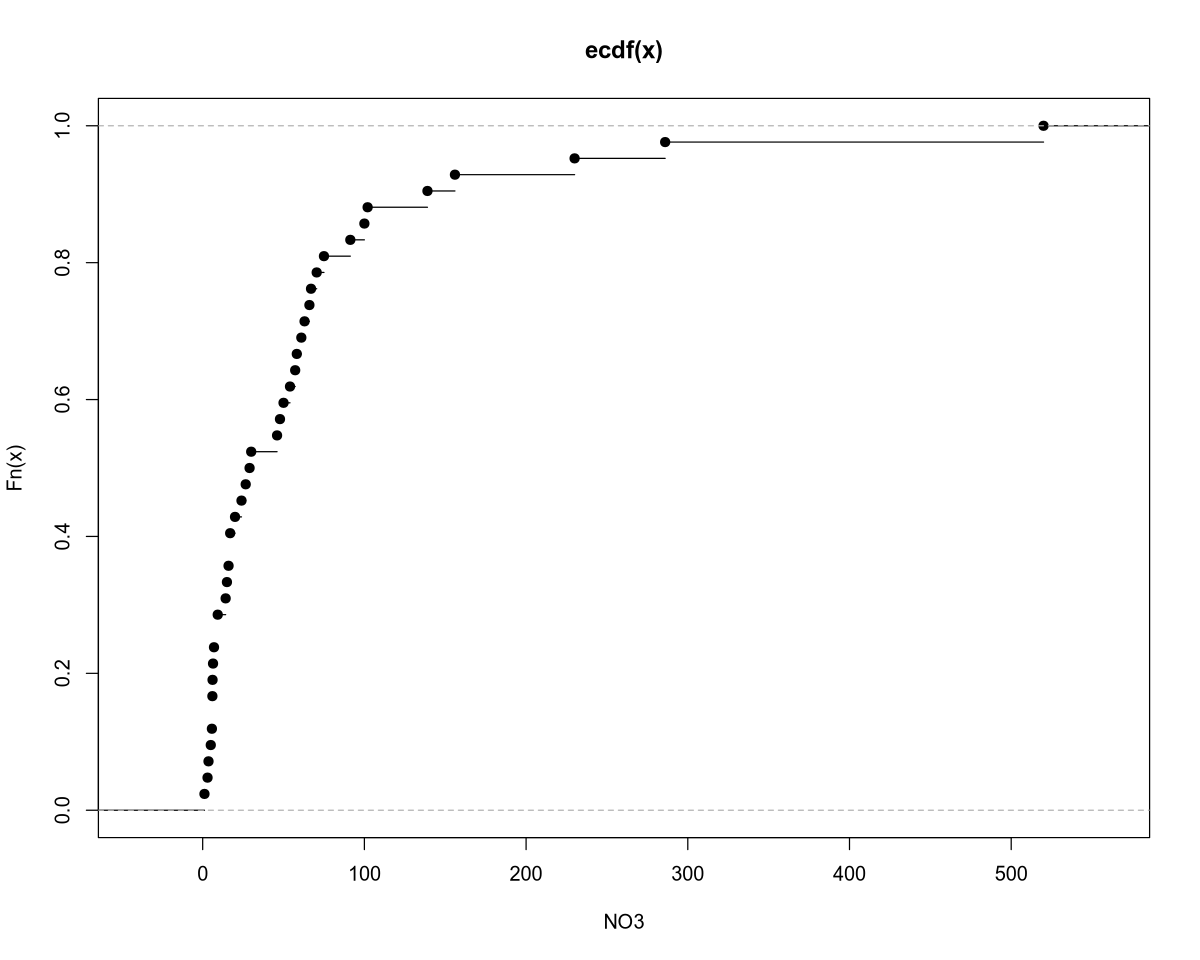
plot.ecdf(NO3, xlab = "NO3")
options(repr.plot.height = 6)
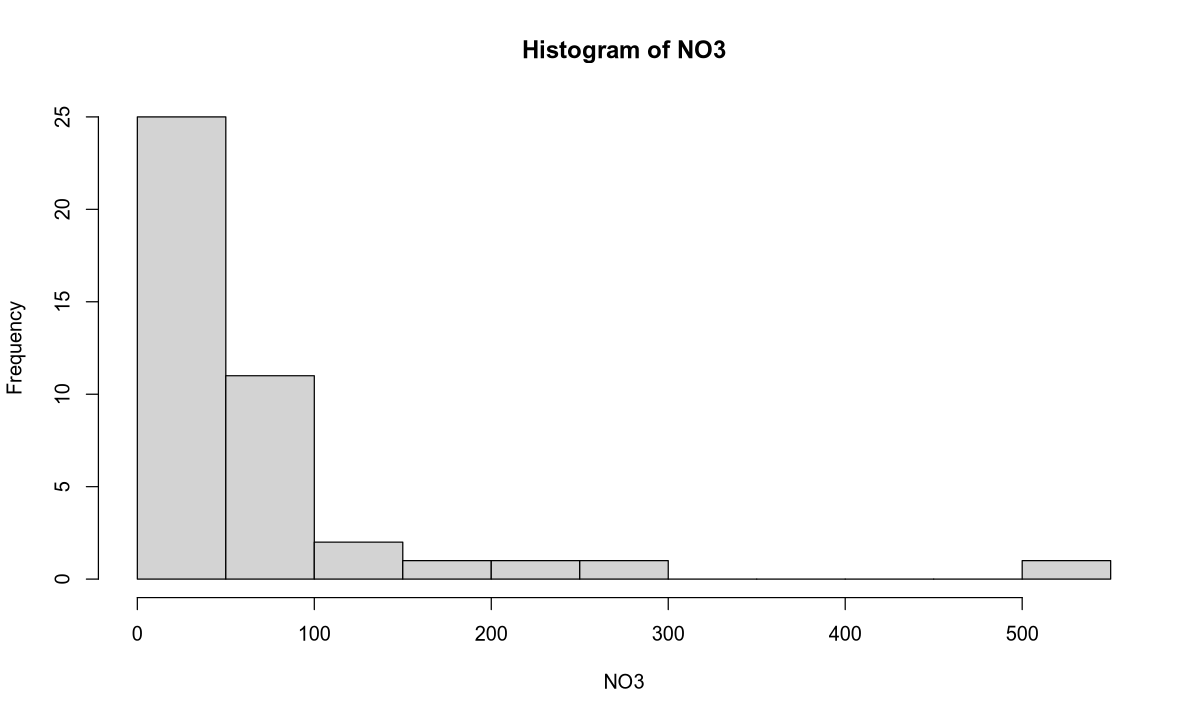
hist(NO3, 18)
options(repr.plot.height = 4)
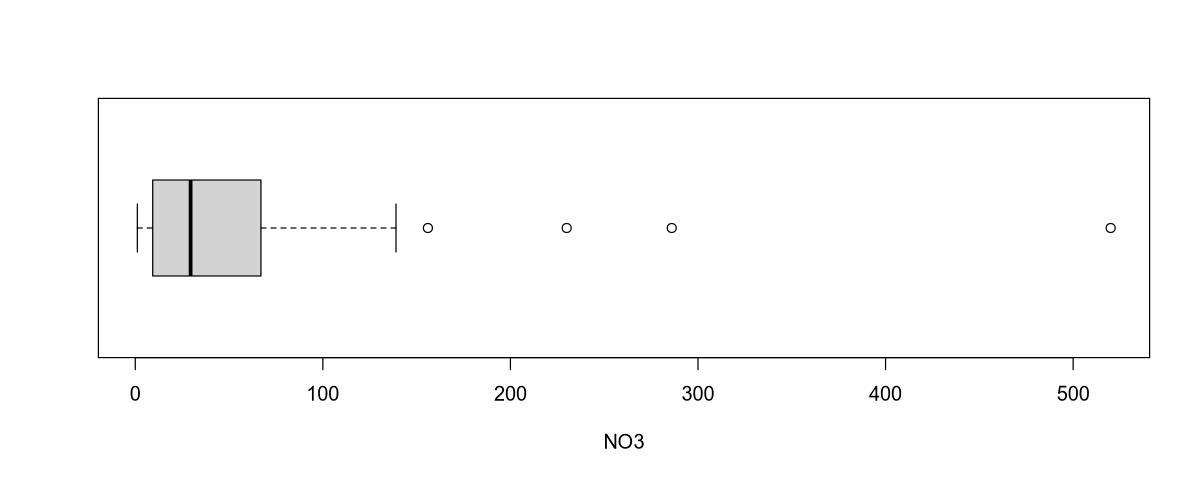
boxplot(NO3, horizontal = T, xlab = "NO3")
cat("Var: ", var(NO3), "\n")
cat("Std: ", sd(NO3), "\n")
summary(NO3)
Var: 8856.962
Std: 94.11144
Min. 1st Qu. Median Mean 3rd Qu. Max.
1.10 9.30 29.50 62.32 66.75 520.00
The mean of the response variable is 62.2, and the median (which is more representative in this case) is 29.5. The sample variance of nitrate concentration is 8857.
Outliers: The nitrate concentration values in the selected rivers range from 1 to 150, with the exception of a few outliers:
| River | Area | NO3 Concentration |
|---|---|---|
| Mersey | England | 156 |
| Meuse | Netherlands/Belgium | 230 |
| Rhine | Europe | 286 |
| Thames | England | 520 |
Population Density
options(repr.plot.width = 10)
options(repr.plot.height = 8)
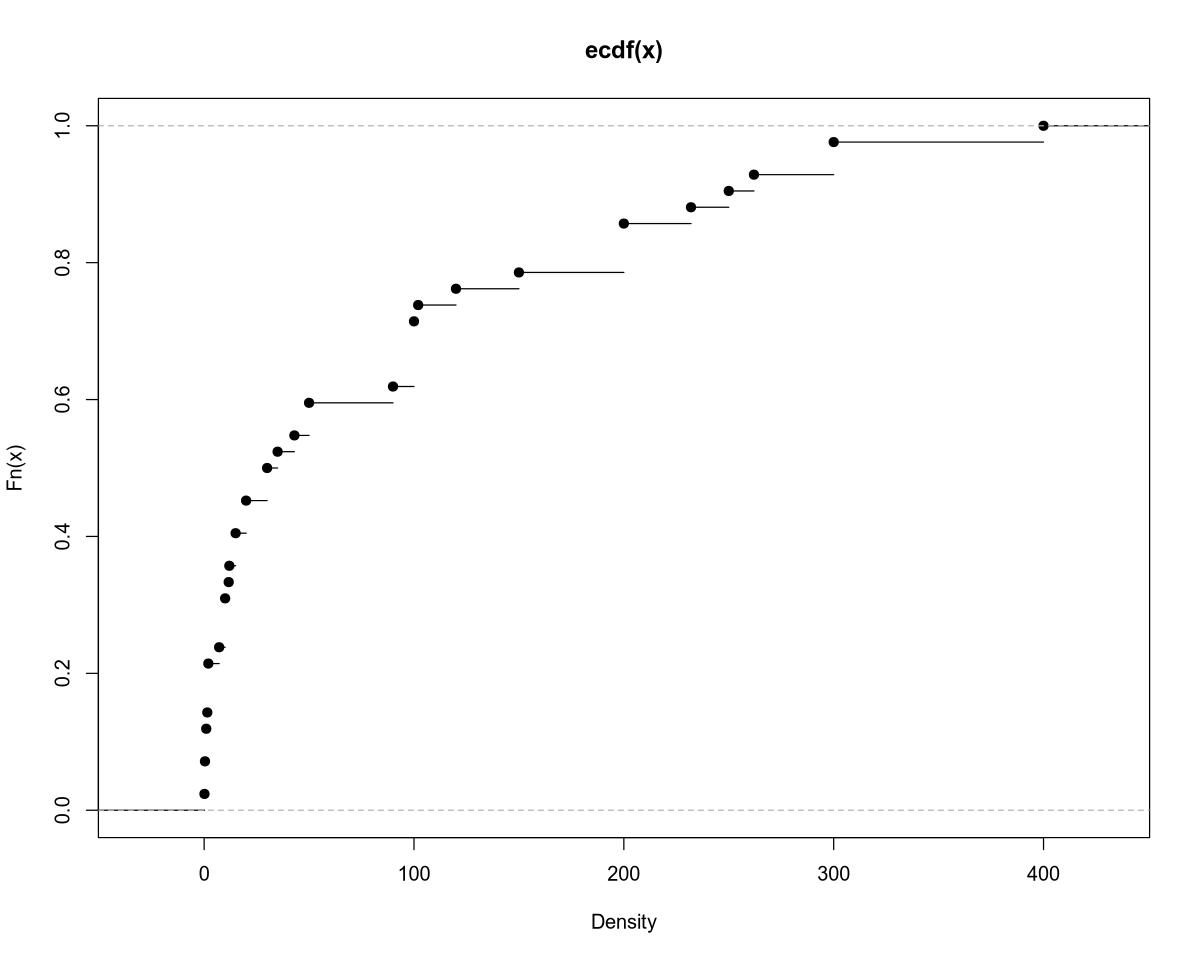
plot.ecdf(Density, xlab = "Density")
options(repr.plot.height = 6)
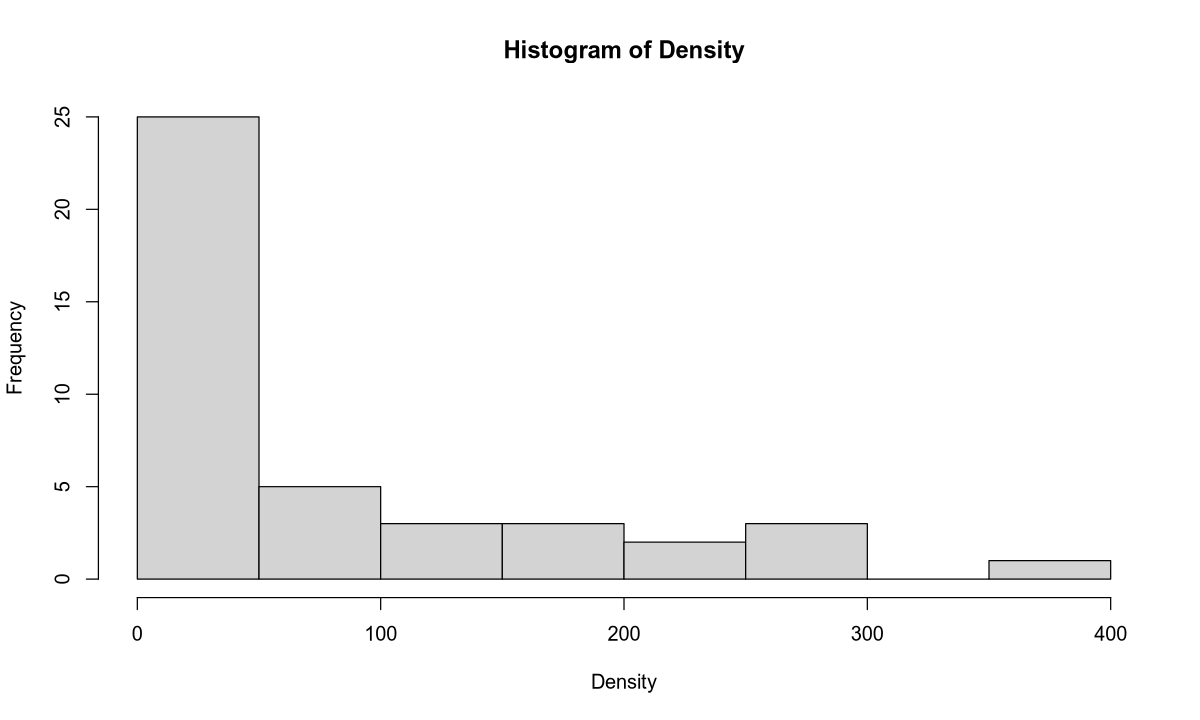
hist(Density, 10)
options(repr.plot.height = 4)
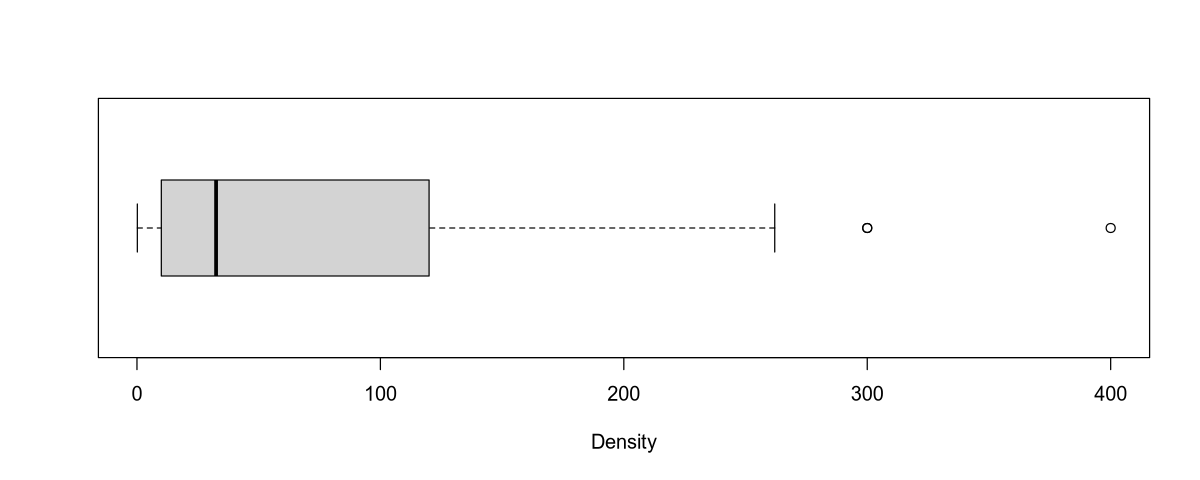
boxplot(Density, horizontal = T, xlab = "Density")
cat("Var: ", var(Density), "\n")
cat("Std: ", sd(Density), "\n")
summary(Density)
Var: 10880.2
Std: 104.3082
Min. 1st Qu. Median Mean 3rd Qu. Max.
0.15 10.00 32.50 85.36 115.50 400.00
Outliers: In the population density data, we observe outliers (similar to NO3 concentration) for rivers flowing through large cities:
| River | Area | Population Density |
|---|---|---|
| Ganges | India | 300.00 |
| Rhine | Europe | 300.00 |
| Thames | England | 400.00 |
Other Explanatory Variables
summary(subset(df, select = c("River", "Country", "Discharge",
"Runoff", "Area", "NPrec", "Prec")))
River Country Discharge Runoff
Length:42 Canada : 5 Min. : 7.29 Min. : 0.20
Class :character USA : 5 1st Qu.: 392.00 1st Qu.: 6.10
Mode :character England : 3 Median : 2050.00 Median :11.85
Italy : 3 Mean : 10342.30 Mean :13.24
Canada/USA: 2 3rd Qu.: 8125.00 3rd Qu.:17.65
China : 2 Max. :175000.00 Max. :45.60
(Other) :22
Area NPrec Prec
Min. : 160 Min. : 1.00 Min. : 15.70
1st Qu.: 43828 1st Qu.: 7.65 1st Qu.: 57.98
Median : 517500 Median :14.85 Median : 89.84
Mean : 937888 Mean :20.79 Mean : 89.84
3rd Qu.:1072250 3rd Qu.:29.73 3rd Qu.:107.10
Max. :7050000 Max. :61.00 Max. :242.10
Interactions Between Variables
options(repr.plot.width = 14, repr.plot.height = 8)
ggpairs(subset(df, select = c("NO3", "Density", "Discharge",
"Runoff", "Area", "NPrec", "Prec")))
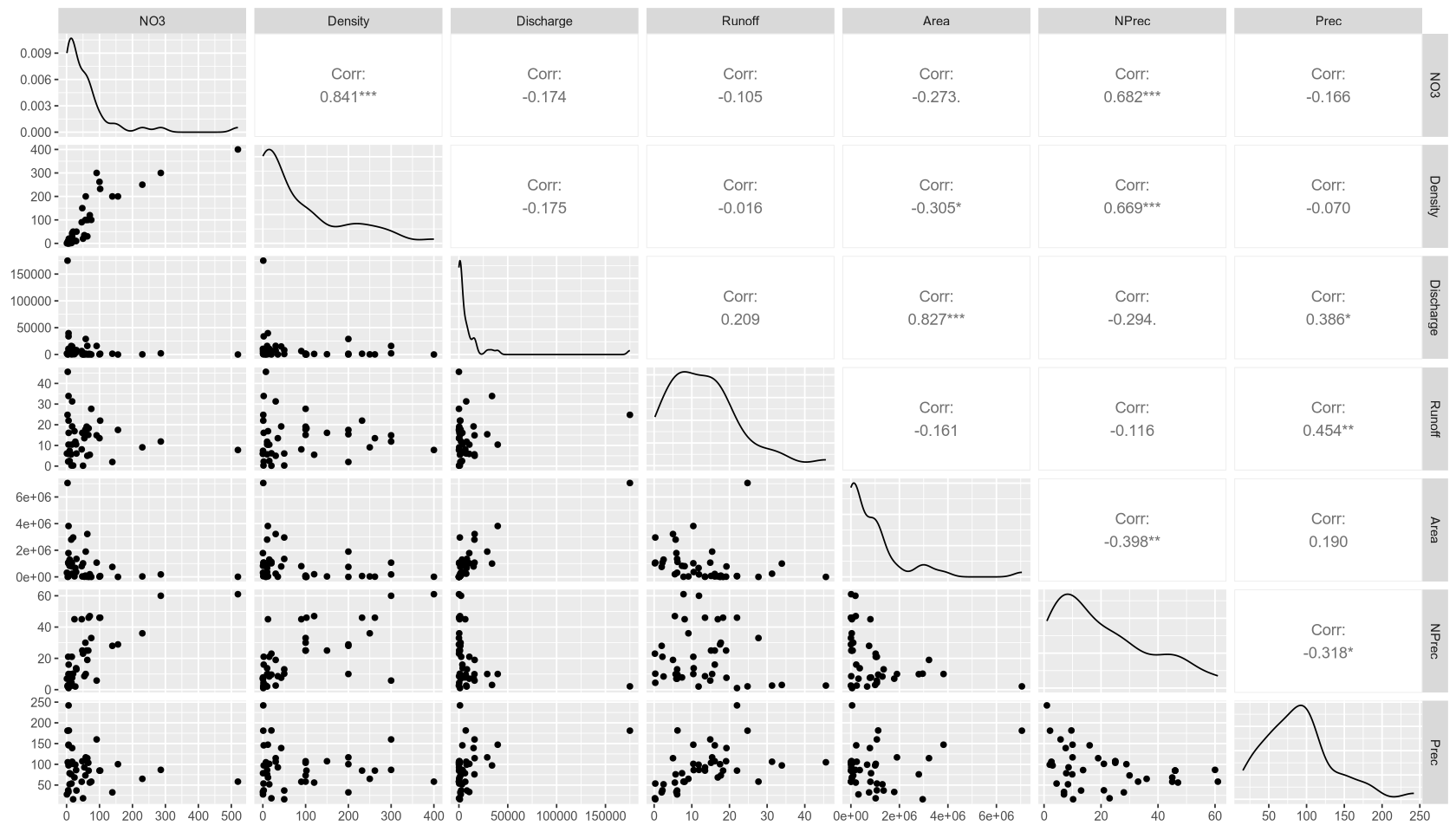
Interesting Interactions:
- We observe a very strong positive correlation of 0.84 between population density (
Density) and NO3 concentration. - Nitrate precipitation (
NPrec) also has a strong positive correlation of 0.68 with NO3 concentration. - We also note a significant positive correlation of 0.67 between
DensityandNPrecthemselves.
Task 2: Simple Linear Regression
Examine the relationship between the response variable and a single numerical regressor (
Density).
We investigate the dependence of NO3 concentration in rivers on population density Density.
fit <- lm(NO3 ~ Density)
summary(fit)
options(repr.plot.width = 14, repr.plot.height = 8)
plot(NO3 ~ Density)
abline(fit)
options(repr.plot.width = 14, repr.plot.height = 5)
par(mfrow = c(1, 2))
plot(fit, which = 1)
plot(fit, which = 3)
Call:
lm(formula = NO3 ~ Density)
Residuals:
Min 1Q Median 3Q Max
-133.880 -11.892 2.416 10.857 218.940
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -2.45705 10.32855 -0.238 0.813
Density 0.75879 0.07718 9.831 3.15e-12 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 51.55 on 40 degrees of freedom
Multiple R-squared: 0.7073, Adjusted R-squared: 0.7
F-statistic: 96.65 on 1 and 40 DF, p-value: 3.148e-12
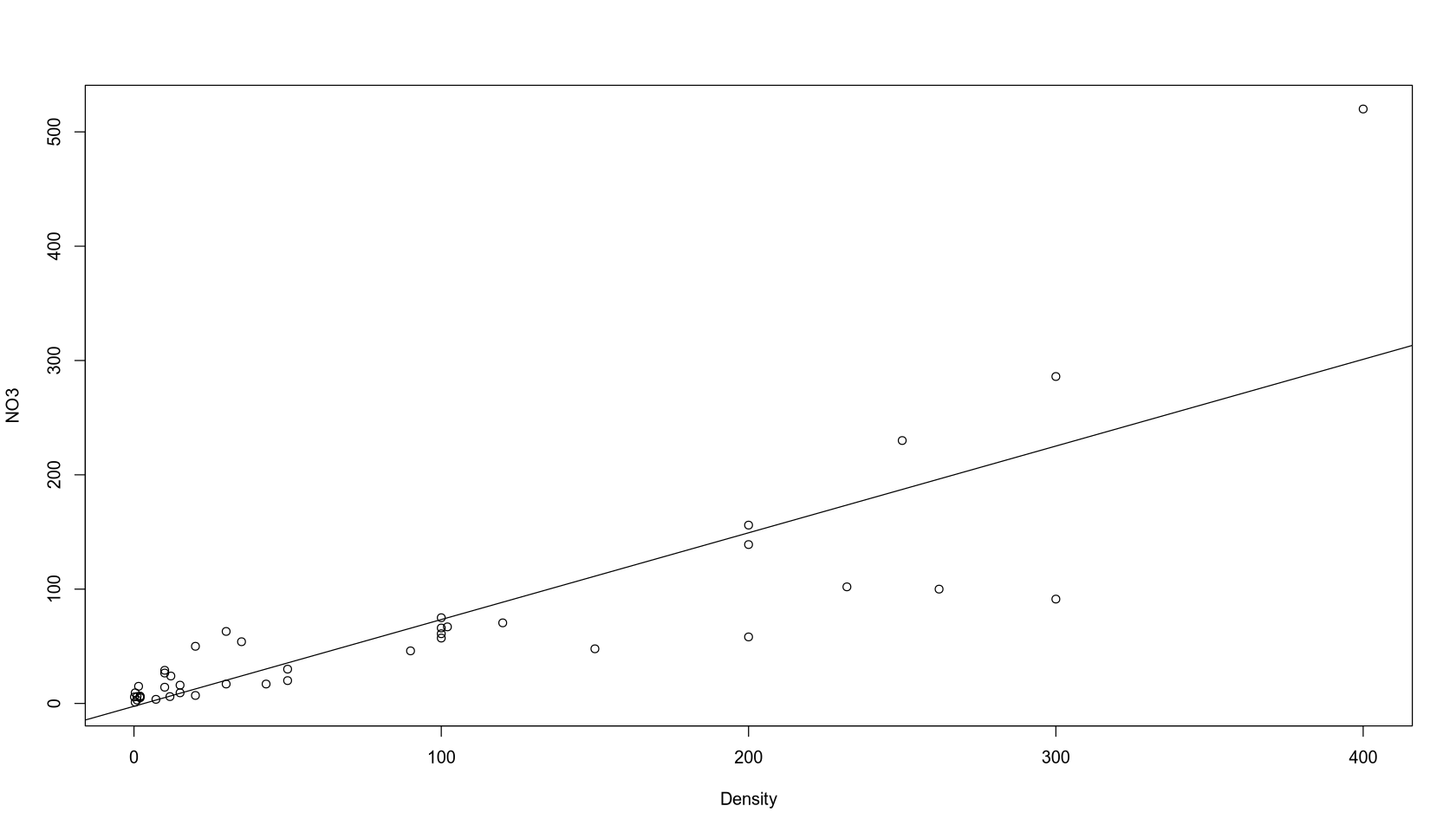
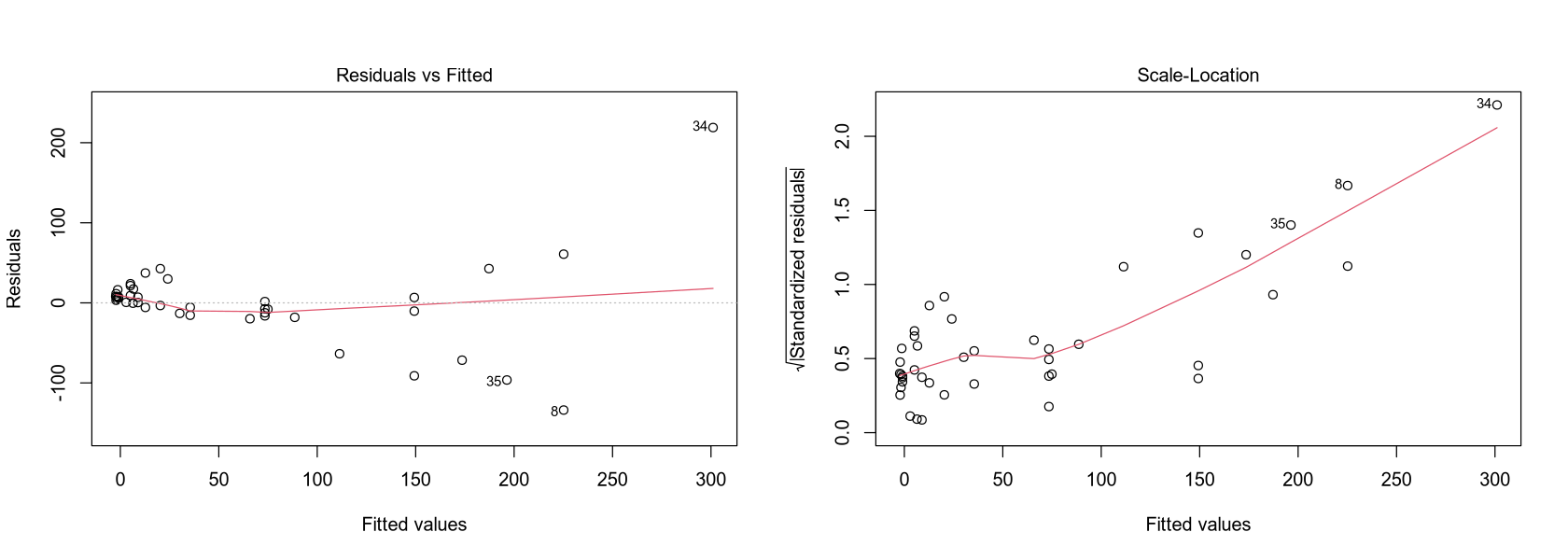
Model Interpretation: A simple linear regression was chosen because the scatter plot shows a linear trend. The adjusted R-squared is 0.70. The intercept is not significant at the 5% level, while the coefficient for Density is highly significant. The model suggests that for every additional person per km², the NO3 concentration increases by 0.7587 micromols/liter. The negative intercept of -2.457 at zero population density is physically unrealistic.
Model Quality: This simple model does not explain the response variable very well. While it doesn’t show systematic errors in the residuals plot, it is inaccurate for higher values, and the intercept is flawed. The data points seem to diverge at higher values, suggesting that a single regression line may not be sufficient. However, the model is very simple and effectively captures the positive relationship between NO3 and Density.
Task 3: Analysis of Variance (ANOVA)
Examine the relationship between the response variable and a single categorical regressor (Continent).
We examine NO3 concentration based on the region where the river flows. We group the regions into the following 4 categories:
- Africa
- America
- Asia-Pacific
- Europe
Continent <- c("Europe", "America", "Europe", "America", "Europe",
"America", "America", "AsiaPacific", "Europe", "AsiaPacific",
"America", "America", "America", "America", "AsiaPacific",
"Europe", "Europe", "America", "AsiaPacific", "America",
"Africa", "Africa", "Africa", "America", "America", "Europe",
"Europe", "Europe", "Europe", "America", "America", "America",
"Europe", "Europe", "Europe", "America", "Europe", "Europe",
"AsiaPacific", "America", "Africa", "Africa")
Continent <- as.factor(Continent)
df$Continent <- Continent
tapply(NO3, Continent, summary)
fit <- lm(NO3 ~ Continent)
summary(fit)
options(repr.plot.width = 14, repr.plot.height = 8)
boxplot(NO3 ~ Continent, ylab = "", xlab = "continent")
options(repr.plot.width = 14, repr.plot.height = 5)
par(mfrow = c(1, 2))
plot(fit, which = 1)
plot(fit, which = 3)
$Africa
Min. 1st Qu. Median Mean 3rd Qu. Max.
6.00 7.00 9.30 18.46 20.00 50.00
$America
Min. 1st Qu. Median Mean 3rd Qu. Max.
1.10 6.00 14.20 22.54 29.00 66.00
$AsiaPacific
Min. 1st Qu. Median Mean 3rd Qu. Max.
15.0 17.0 58.2 64.1 91.3 139.0
$Europe
Min. 1st Qu. Median Mean 3rd Qu. Max.
3.6 50.0 70.5 121.4 129.0 520.0
Call:
lm(formula = NO3 ~ Continent)
Residuals:
Min 1Q Median 3Q Max
-117.82 -40.18 -12.85 20.56 398.58
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 18.460 37.990 0.486 0.6298
ContinentAmerica 4.081 43.217 0.094 0.9253
ContinentAsiaPacific 45.640 53.725 0.850 0.4009
ContinentEurope 102.960 43.867 2.347 0.0242 *
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 84.95 on 38 degrees of freedom
Multiple R-squared: 0.2449, Adjusted R-squared: 0.1853
F-statistic: 4.108 on 3 and 38 DF, p-value: 0.0128
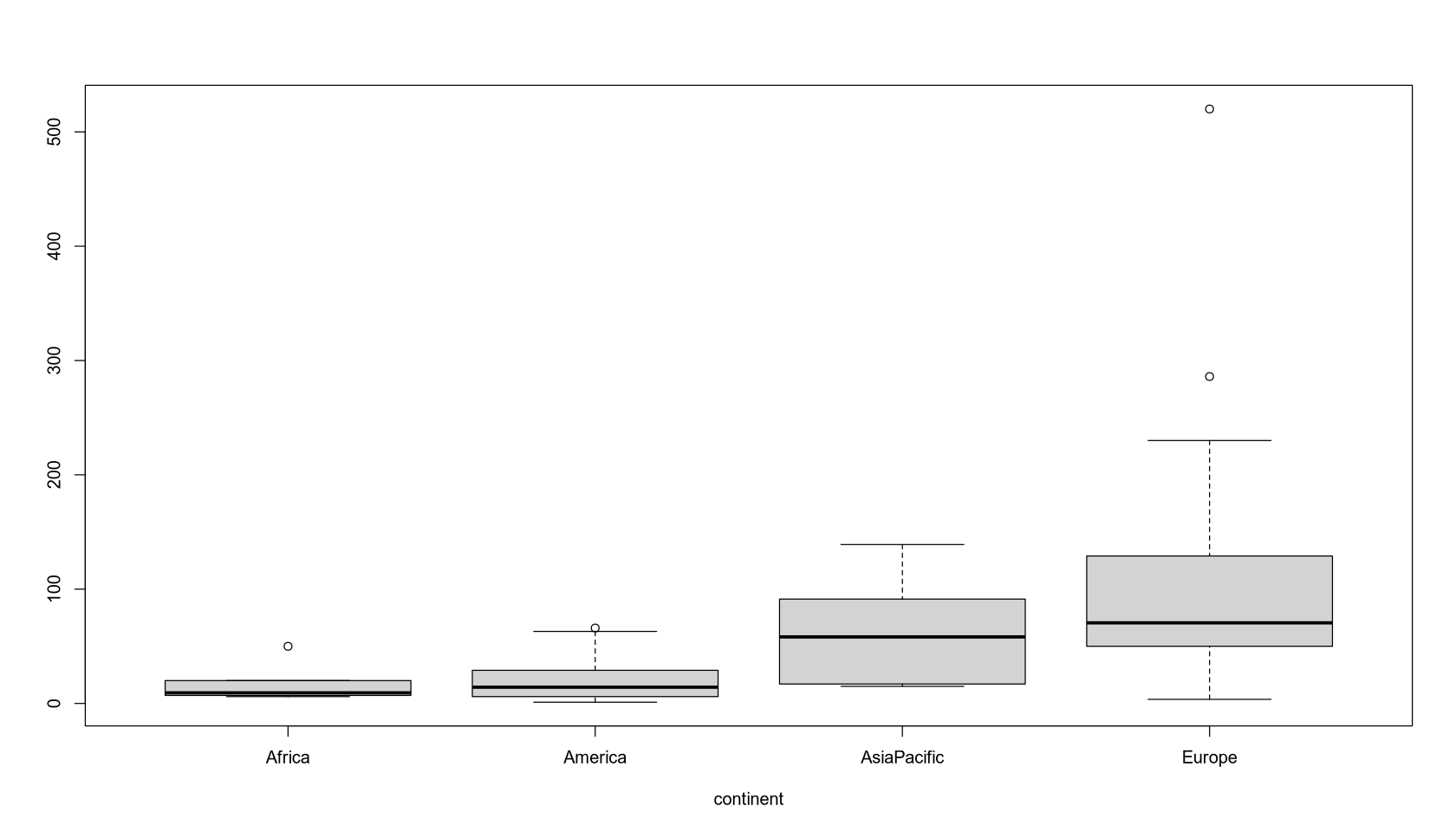
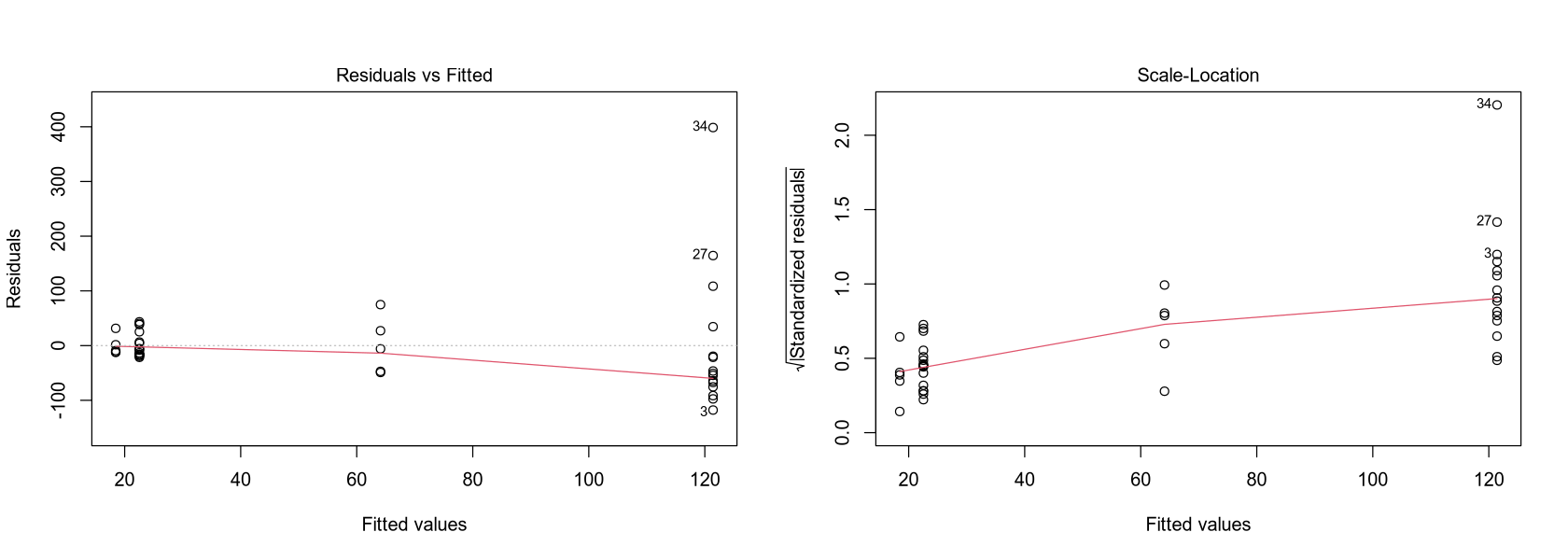
Observation: NO3 concentration in Africa and the Americas is significantly lower than in Europe and the Asia-Pacific region.
Test: We test if the mean NO3 concentration is the same for all continents.
\(H_0 : \mu_\text{Africa} = \mu_\text{America} = \mu_\text{AsiaPacific} = \mu_\text{Europe}\)
\(H_A : \text{Not } H_0\)
aov(NO3 ~ Continent)
anova(aov(NO3 ~ Continent))
Call:
aov(formula = NO3 ~ Continent)
Terms:
Continent Residuals
Sum of Squares 88926.52 274208.94
Deg. of Freedom 3 38
Residual standard error: 84.94719
Estimated effects may be unbalanced
| Df | Sum Sq | Mean Sq | F value | Pr(>F) | |
|---|---|---|---|---|---|
| <int> | <dbl> | <dbl> | <dbl> | <dbl> | |
| Continent | 3 | 88926.52 | 29642.174 | 4.107826 | 0.01280309 |
| Residuals | 38 | 274208.94 | 7216.025 | NA | NA |
Conclusion: At a 5% significance level, we reject the null hypothesis, concluding that the mean NO3 concentration differs by continent. We see that the concentration is highest in Europe, slightly lower in the Asia-Pacific region, and significantly lower in the Americas and Africa.
Interpretation: The average NO3 concentration is 18.46 in Africa, 22.54 in America, 64.1 in AsiaPacific, and 121.4 in Europe. At the 5% level, only the coefficient for Europe is significant relative to the baseline (Africa).
Model Quality: The model evaluating the mean values for each continent is usable but very coarse. It doesn’t provide a complete picture, especially for Europe and the Asia-Pacific region, where the variance is large.
Task 4: Interaction Model
Consider a regression model containing both previous regressors (
DensityandContinent) including their interaction.
fit <- lm(NO3 ~ Density + Density:Continent)
summary(fit)
options(repr.plot.width = 14, repr.plot.height = 8)
tmp <- suppressWarnings(predict(fit, interval = "prediction"))
ggplot(cbind(df, tmp), aes(x = Density, y = NO3, group = Continent, color = Continent)) +
geom_point() + geom_line(aes(y = fit)) + theme_bw()
options(repr.plot.width = 14, repr.plot.height = 5)
par(mfrow = c(1, 2))
plot(fit, which = 1)
plot(fit, which = 3)
Call:
lm(formula = NO3 ~ Density + Density:Continent)
Residuals:
Min 1Q Median 3Q Max
-130.834 -14.438 2.416 11.910 168.013
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 0.8182 9.7710 0.084 0.934
Density 0.6156 0.7971 0.772 0.445
Density:ContinentAmerica -0.1054 0.7915 -0.133 0.895
Density:ContinentAsiaPacific -0.2259 0.7888 -0.286 0.776
Density:ContinentEurope 0.2623 0.7842 0.335 0.740
Residual standard error: 44.4 on 37 degrees of freedom
Multiple R-squared: 0.7991, Adjusted R-squared: 0.7774
F-statistic: 36.8 on 4 and 37 DF, p-value: 2.005e-12
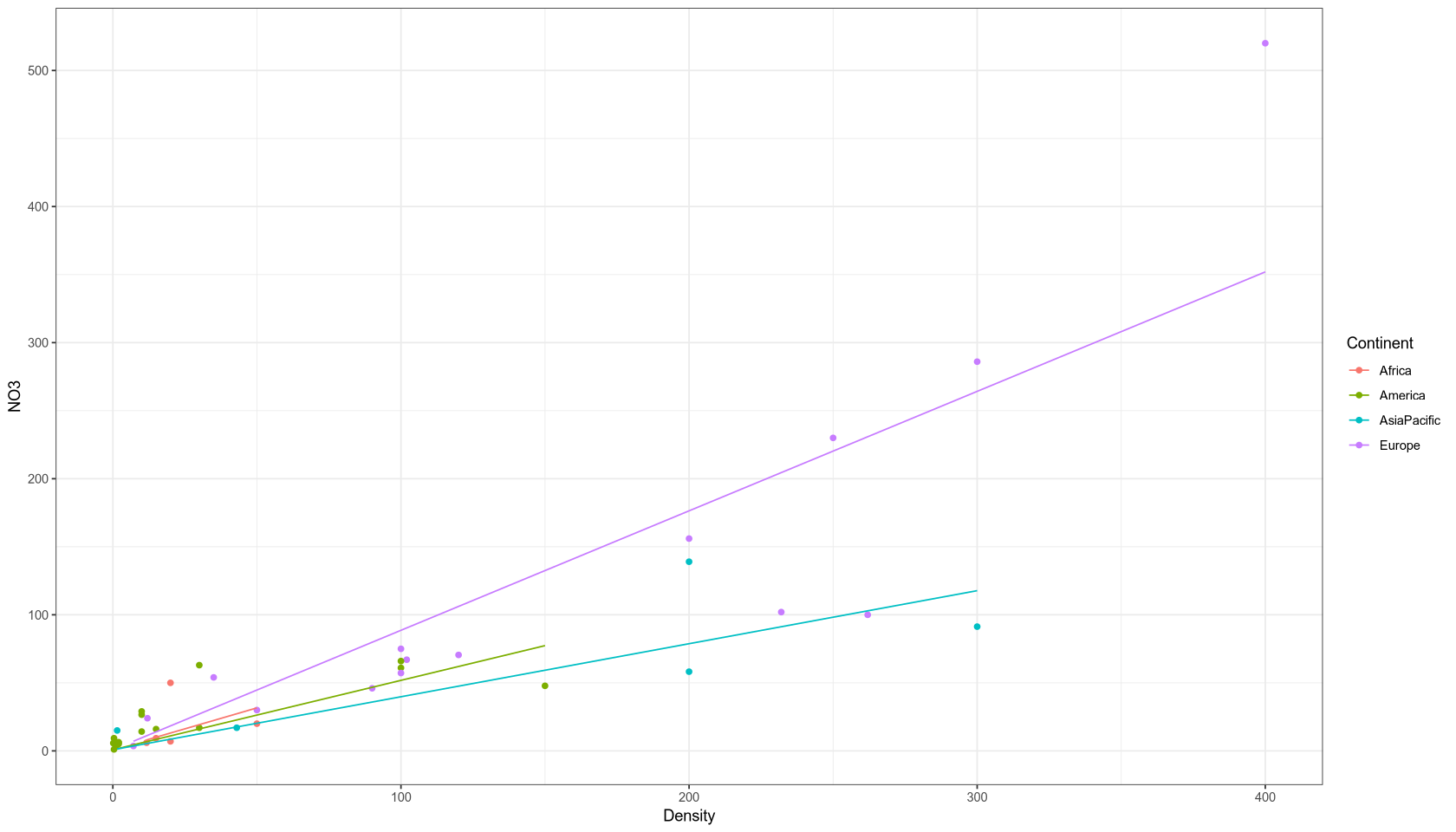
Assumption: The NO3 concentration at zero population density (Density = 0) is the same on all continents. We chose the model lm(NO3 ~ Density + Density:Continent) which reflects this assumption by allowing different slopes for each continent but a common intercept.
Interpretation: The adjusted R-squared is 0.78. At zero population density, the natural NO3 concentration is 0.8182 micromol/liter. For each additional person per km², the NO3 concentration increases by the following amounts (in micromols NO3 per liter):
| Continent | Calculation | Coefficient |
|---|---|---|
| Asia-Pacific | 0.6156 - 0.2259 | 0.3897 |
| America | 0.6156 - 0.1054 | 0.5102 |
| Africa | 0.6156 (base) | 0.6156 |
| Europe | 0.6156 + 0.2623 | 0.8779 |
Result: All coefficients are insignificant at the 5% level. This suggests the model might be over-parameterized and could be simplified.
Model Quality: This model explains the response variable slightly better than the previous regressions, as it accounts for continents and is more flexible at higher values. However, it is much more complex and still inaccurate at high values.
Task 5: Final Model Selection
Find a suitable final model that explains the behavior well but does not contain insignificant components.
Approach: We will start with a complex model including all regressors and then simplify it sequentially. The goal is a model that explains the data well without unnecessary complexity.
Initial Model: We start with a model containing the previous two regressors plus other features from the dataset. We also add NPrec:Continent and Prec:Continent interactions, as precipitation might have different effects on NO3 concentration in different regions.
fit_overparam <- lm(NO3 ~ Density + Density:Continent + Continent +
Discharge + Runoff + Area + NPrec + NPrec:Continent + Prec + Prec:Continent)
summary(fit_overparam)
Call:
lm(formula = NO3 ~ Density + Density:Continent + Continent +
Discharge + Runoff + Area + NPrec + NPrec:Continent + Prec +
Prec:Continent)
Residuals:
Min 1Q Median 3Q Max
-126.862 -9.479 -1.329 7.749 130.537
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -1.741e+01 1.241e+02 -0.140 0.890
Density 2.456e-02 2.093e+00 0.012 0.991
ContinentAmerica 1.611e+01 1.275e+02 0.126 0.901
ContinentAsiaPacific 2.587e+01 1.563e+02 0.166 0.870
ContinentEurope 6.059e+01 1.387e+02 0.437 0.666
Discharge -2.048e-04 7.873e-04 -0.260 0.797
Runoff 1.420e-01 1.406e+00 0.101 0.920
Area 3.116e-06 1.657e-05 0.188 0.852
NPrec 2.796e+00 5.009e+00 0.558 0.582
Prec -4.542e-02 4.546e-01 -0.100 0.921
Density:ContinentAmerica 2.757e-01 2.160e+00 0.128 0.900
Density:ContinentAsiaPacific 2.764e-01 2.107e+00 0.131 0.897
Density:ContinentEurope 1.070e+00 2.101e+00 0.509 0.615
ContinentAmerica:NPrec -2.157e+00 5.491e+00 -0.393 0.698
ContinentAsiaPacific:NPrec -2.336e-01 6.618e+00 -0.035 0.972
ContinentEurope:NPrec -3.493e+00 5.098e+00 -0.685 0.500
ContinentAmerica:Prec 9.982e-02 5.189e-01 0.192 0.849
ContinentAsiaPacific:Prec -1.558e-01 9.208e-01 -0.169 0.867
ContinentEurope:Prec -8.138e-01 9.178e-01 -0.887 0.384
Residual standard error: 49.12 on 23 degrees of freedom
Multiple R-squared: 0.8472, Adjusted R-squared: 0.7276
F-statistic: 7.083 on 18 and 23 DF, p-value: 1.216e-05
Observation: The R-squared of 0.8472 is very good, but all coefficients are insignificant, so we should simplify the model.
Model-Submodel Test: We use a stepwise selection process (based on AIC) to reduce the full model.
step(lm(NO3 ~ 1), trace=T, scope = list(
lower = ~1,
upper = ~NO3 ~ Density + Density:Continent + Continent + Discharge + Runoff + Area + NPrec + NPrec:Continent + Prec + Prec:Continent
))
Start: AIC=382.72
NO3 ~ 1
Df Sum of Sq RSS AIC
+ Density 1 256842 106294 333.12
+ NPrec 1 168973 194163 358.43
+ Continent 3 88927 274209 376.93
+ Area 1 27124 336011 381.46
<none> 363135 382.72
+ Discharge 1 11001 352134 383.43
+ Prec 1 10049 353087 383.55
+ Runoff 1 3984 359151 384.26
Step: AIC=333.12
NO3 ~ Density
Df Sum of Sq RSS AIC
+ NPrec 1 9395 96899 331.24
<none> 106294 333.12
+ Prec 1 4244 102050 333.41
+ Continent 3 12904 93390 333.69
+ Runoff 1 3034 103259 333.91
+ Discharge 1 269 106024 335.02
+ Area 1 113 106180 335.08
- Density 1 256842 363135 382.72
Step: AIC=331.24
NO3 ~ Density + NPrec
Df Sum of Sq RSS AIC
<none> 96899 331.24
+ Runoff 1 1744 95154 332.47
+ Prec 1 1014 95885 332.80
+ Area 1 275 96624 333.12
- NPrec 1 9395 106294 333.12
+ Discharge 1 53 96846 333.21
+ Continent 3 6137 90762 334.49
- Density 1 97264 194163 358.43
Call:
lm(formula = NO3 ~ Density + NPrec)
Coefficients:
(Intercept) Density NPrec
-16.1835 0.6282 1.1965
fit_reduced_1 <- lm(NO3 ~ Density + NPrec)
summary(fit_reduced_1)
Call:
lm(formula = NO3 ~ Density + NPrec)
Residuals:
Min 1Q Median 3Q Max
-103.440 -14.440 2.526 17.014 211.923
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -16.1835 12.2300 -1.323 0.1935
Density 0.6282 0.1004 6.257 2.28e-07 ***
NPrec 1.1965 0.6153 1.945 0.0591 .
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 49.85 on 39 degrees of freedom
Multiple R-squared: 0.7332, Adjusted R-squared: 0.7195
F-statistic: 53.58 on 2 and 39 DF, p-value: 6.484e-12
Commentary: The stepwise algorithm stopped at the model with the lowest AIC: NO3 ~ Density + NPrec. However, this model still has insignificant components at the 5% level, which we will now remove manually.
# remove intercept
fit_reduced_2 <- lm(NO3 ~ 0 + Density + NPrec)
summary(fit_reduced_2)
Call:
lm(formula = NO3 ~ 0 + Density + NPrec)
Residuals:
Min 1Q Median 3Q Max
-101.327 -18.167 -6.716 4.405 224.464
Coefficients:
Estimate Std. Error t value Pr(>|t|)
Density 0.6280 0.1013 6.197 2.49e-07 ***
NPrec 0.7265 0.5072 1.433 0.16
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 50.31 on 40 degrees of freedom
Multiple R-squared: 0.8076, Adjusted R-squared: 0.798
F-statistic: 83.95 on 2 and 40 DF, p-value: 4.833e-15
# remove NPrec
fit_reduced_3 <- lm(NO3 ~ 0 + Density)
summary(fit_reduced_3)
Call:
lm(formula = NO3 ~ 0 + Density)
Residuals:
Min 1Q Median 3Q Max
-132.824 -12.885 0.547 8.433 221.168
Coefficients:
Estimate Std. Error t value Pr(>|t|)
Density 0.74708 0.05875 12.72 8.15e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 50.95 on 41 degrees of freedom
Multiple R-squared: 0.7977, Adjusted R-squared: 0.7928
F-statistic: 161.7 on 1 and 41 DF, p-value: 8.151e-16
Quality Comparison: It is interesting to track the R-squared values during this simplification process.
| Fit | Model | R-squared | Adjusted R-squared |
|---|---|---|---|
| fit_overparam | NO3 ~ … | 0.8472 | 0.7276 |
| fit_reduced_1 | NO3 ~ Density + NPrec | 0.7332 | 0.7195 |
| fit_reduced_2 | NO3 ~ 0 + Density + NPrec | 0.8076 | 0.7980 |
| fit_reduced_3 | NO3 ~ 0 + Density | 0.7977 | 0.7928 |
The highest adjusted R-squared (which accounts for the number of parameters) belongs to fit_reduced_2. However, fit_reduced_3 is simpler and only marginally worse.
anova(fit_reduced_3,
fit_reduced_2,
fit_reduced_1,
fit_overparam,
test="F")
| Res.Df | RSS | Df | Sum of Sq | F | Pr(>F) | |
|---|---|---|---|---|---|---|
| <dbl> | <dbl> | <dbl> | <dbl> | <dbl> | <dbl> | |
| 1 | 41 | 106444.01 | NA | NA | NA | NA |
| 2 | 40 | 101249.30 | 1 | 5194.707 | 2.152962 | 0.1558373 |
| 3 | 39 | 96898.70 | 1 | 4350.605 | 1.803121 | 0.1924385 |
| 4 | 23 | 55494.84 | 16 | 41403.858 | 1.072497 | 0.4293205 |
Model-Submodel Test Result: The F-test shows that there is no statistically significant difference between the models. Therefore, we can reduce the more complex models to the final model fit_reduced_3 (NO3 ~ 0 + Density).
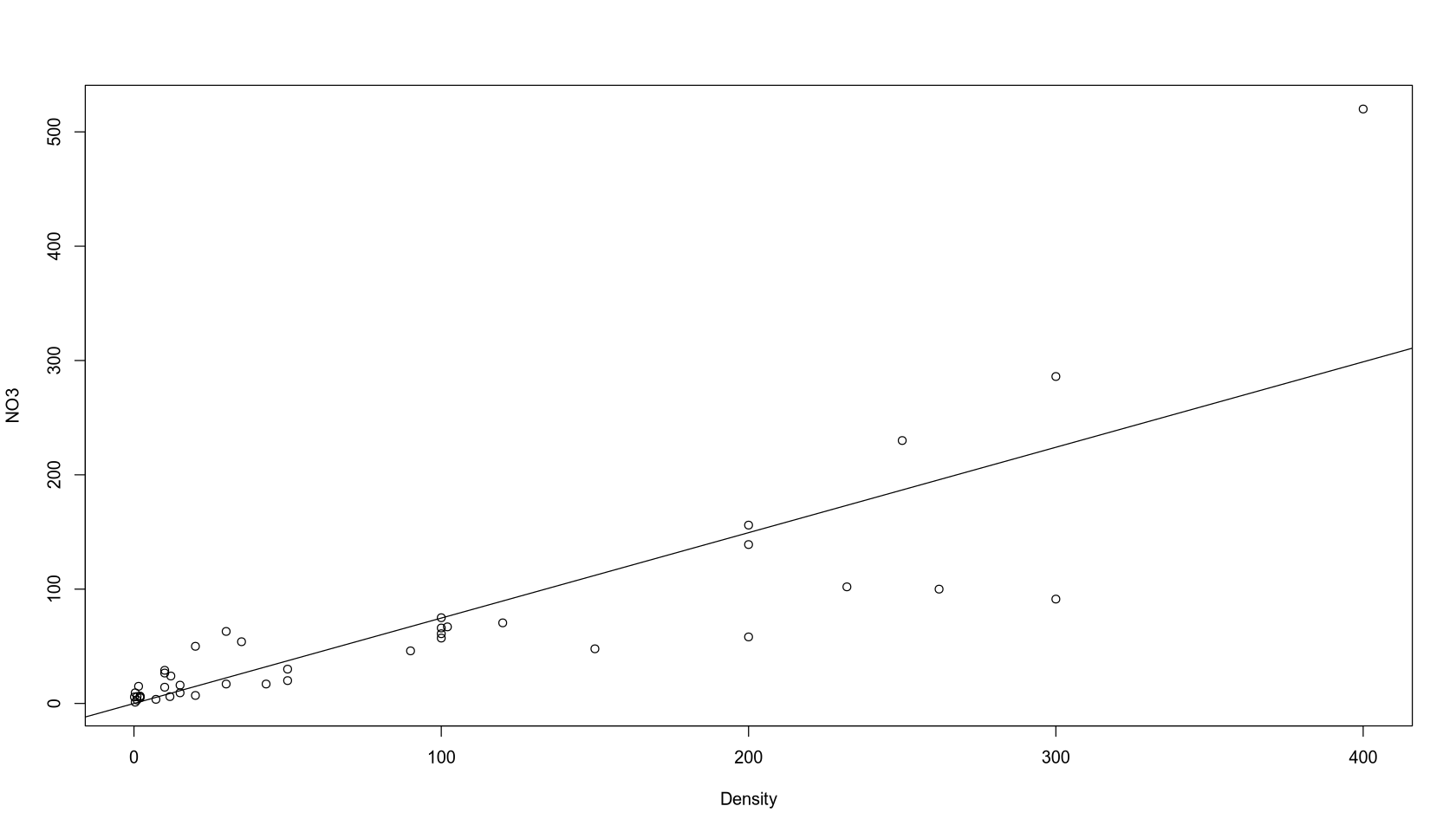
Final Model Interpretation: At zero population density, the natural NO3 concentration is zero, and with each additional person per km², it increases by 0.74708 micromols per liter.
Final Model Quality: Like the other models, it is inaccurate at higher values. On the other hand, it is easily interpretable and, importantly, it has a permissible NO3 concentration value (non-negative) at Density = 0.
options(repr.plot.width = 14, repr.plot.height = 8)
plot(NO3 ~ 0 + Density)
abline(fit_reduced_3)
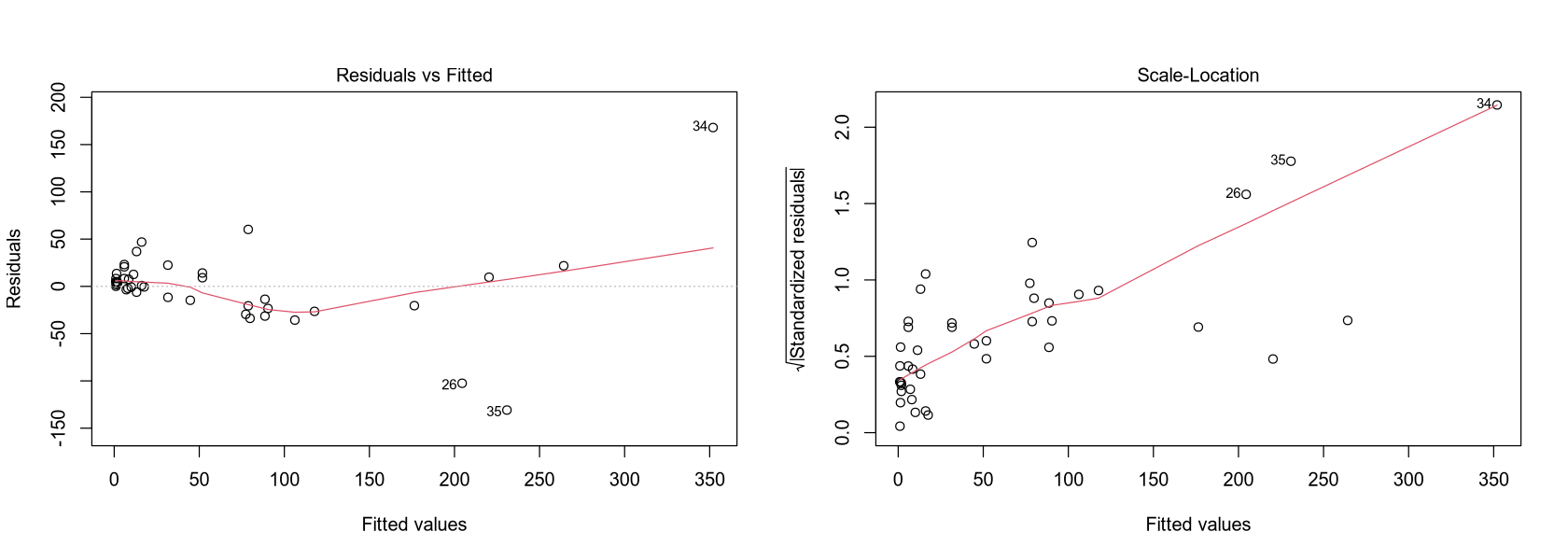
Task 6: Verification of Model Assumptions
For the final model, verify the assumptions of the methods used with appropriate tests.
fit_residual <- lm(NO3 ~ Density + Density:Continent + Continent +
Discharge + Runoff + Area + NPrec + NPrec:Continent + Prec + Prec:Continent)
residuals <- resid(fit_residual)
options(repr.plot.width = 14, repr.plot.height = 5)
par(mfrow = c(1, 2))
plot(residuals)
hist(residuals)
plot(fit, which = 1)
plot(fit, which = 3)
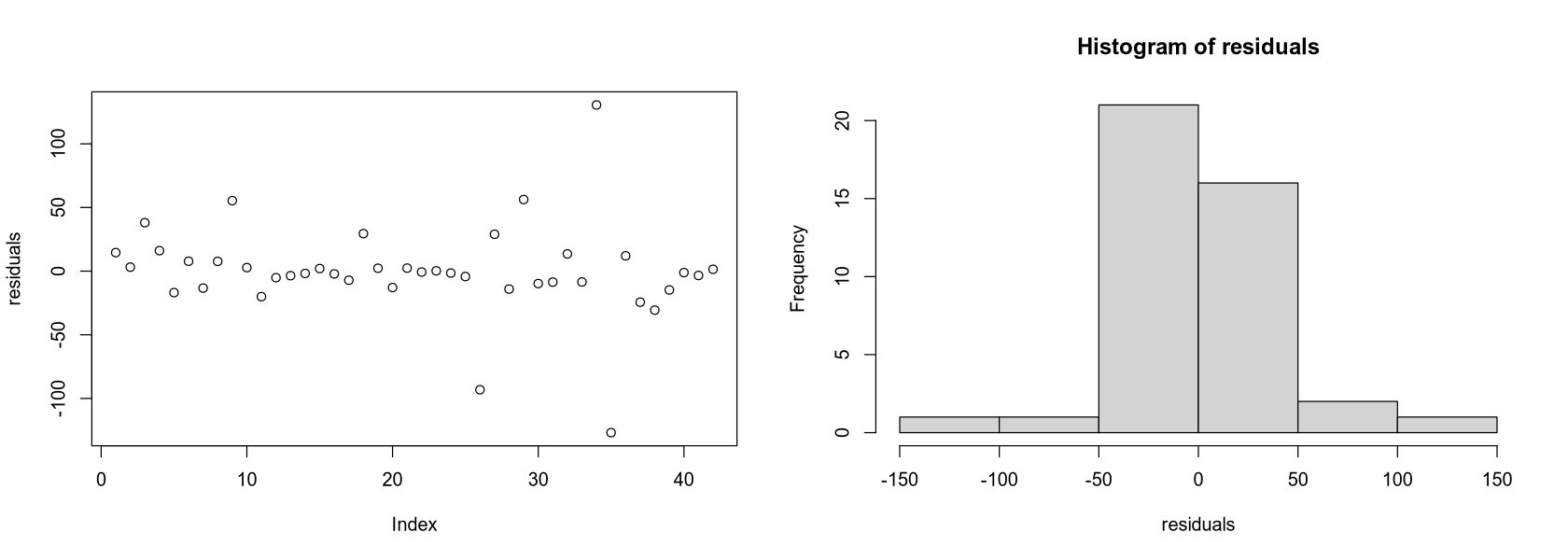
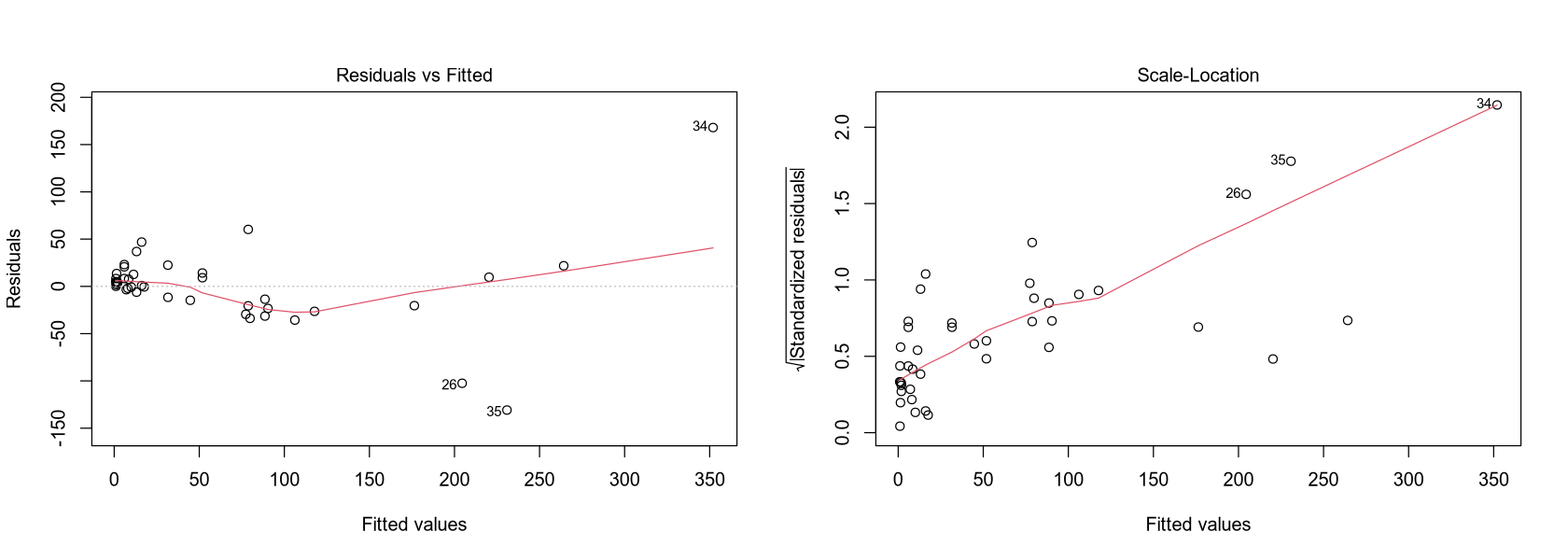
To use the previous diagnostic methods, several assumptions must be verified.
Regression Model: Requires, in addition to a linear relationship, independent and identically distributed errors.
Analysis of Variance (ANOVA): Similar to LR, requires independence, homogeneity of variances, and, for the model selection method, normality of errors.
Normality of Residuals
The residuals plot shows they are distributed quite symmetrically around zero, but their center is not a straight line parallel to the x-axis.
Test: We examine the normality of the residuals using a Q-Q plot and the Shapiro-Wilk normality test:
\(H_0 :\) The residuals come from a normal distribution.
\(H_A :\) The residuals do not come from a normal distribution.
shapiro.test(residuals)
options(repr.plot.width = 10, repr.plot.height = 6)
plot(fit_residual, which = 2)
Shapiro-Wilk normality test
data: residuals
W = 0.79481, p-value = 3.439e-06
Conclusion (Shapiro-Wilk, Q-Q): At a 5% significance level, we reject the null hypothesis that the residuals come from a normal distribution. The result is consistent with the Q-Q plot, where the values of low and high quantiles differ significantly from normal. The assumptions for using linear regression and ANOVA methods were not met.
Solution: In linear regression, we can estimate parameters using the method of least squares and approximately test the significance of regressors using the T-statistic. For ANOVA, the Kruskal-Wallis test can be used, which can identify differences between several categories without assuming normality of residuals.
Homoscedasticity of Residuals
Test: We test the homogeneity of residual variances with the Breusch-Pagan test.
\(H_0 :\) The residuals have constant variance.
\(H_A :\) The residuals do not have constant variance.
bptest(fit_residual)
studentized Breusch-Pagan test
data: fit_residual
BP = 20.876, df = 18, p-value = 0.2857
Conclusion (BP test): At a 5% significance level, we do not reject the homogeneity of variances for the initial model.
bptest(fit_reduced_1)
studentized Breusch-Pagan test
data: fit_reduced_1
BP = 17.647, df = 2, p-value = 0.0001472
However, after the first reduction, this assumption is violated, and the residuals no longer have constant variance (we would reject the test). This is evident in the plots, where the data is clearly heteroscedastic. In such a case, it is possible to transform the response variable, for example, using a Box-Cox transformation.
Other Assumptions
Multicollinearity: The matrix \(\mathbf{X}^T\mathbf{X}\) can be singular or ill-conditioned, and its inverse may not exist, or the coefficient estimates may have high variance. In the initial analysis of fit_overparam, we observed a high correlation between Area and Discharge or NPrec and Density. In such a case, we could opt for ridge regression, which introduces a bias to improve the matrix’s condition.
However, we do not encounter a multicollinearity problem with our final model, as we use only one regressor without an intercept (making \(\mathbf{X}^T\mathbf{X}\) a 1x1 matrix).
Outliers: Outliers are problematic because they can strongly influence the final model. In our case, the outliers are relatively symmetrically distributed (caused by heteroscedasticity), but if we wanted a more robust model estimate, robust regression would be a suitable option.
detach(ex1221)