 image source: DeepMind blog article
image source: DeepMind blog article
This scientific project develops an interpretable model for classifying protein sequences into the most common protein families found in the UniProt Knowledgebase. The study employs common NLP techniques and compares various machine learning models, such as k-nearest neighbors, decision trees, and random forests.
Preliminaries
Amino acids
Amino acids are the basic building blocks of proteins. With few exceptions, all proteins in all living organisms are composed of 19 types of primary amino acids and one secondary amino acid. (P). [🔗]
| Glycine (G) | Alanine (A) | Proline (P) | Valine (V) | Leucine (L) |
| Isoleucine (I) | Methionine (M) | Phenylalanine (F) | Tyrosine (Y) | Tryptophan (W) |
| Serine (S) | Threonine (T) | Cysteine (C) | Asparagine (N) | Glutamine (Q) |
| Lysine (K) | Histidine (H) | Arginine (R) | Aspartate (D) | Glutamate (E) |
Proteins
Proteins are the basis of all known organisms and perform many functions in the body. Each protein is made up of a long chain of amino acid residues that uniquely determines the shape of the protein, which in turn determines its function. [🔗]
Protein structures
The structure of protein chains is distinguished into primary, secondary, tertiary and, for some more complex proteins, quaternary. The primary structure is determined by the order of amino acids in the chain. It also uniquely determines all higher structures. [🔗]
| Primary | Secondary | Tertiary | Quaternary |
|---|---|---|---|
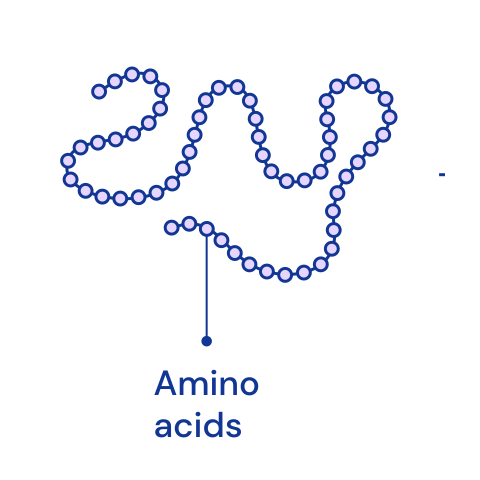 | 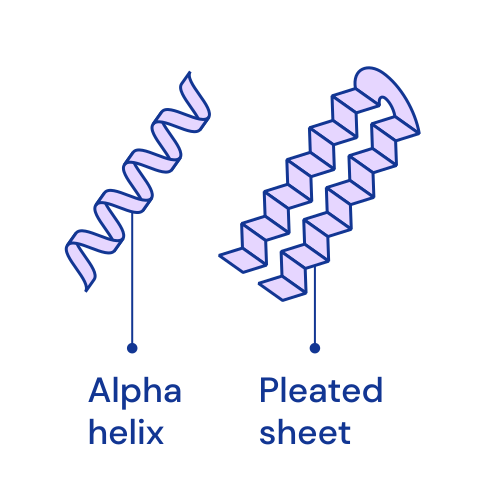 |  |  |
Protein family
A protein family is a group of evolutionarily related proteins that typically have similar three-dimensional structure (tertiary structure), function, and significant sequence similarity. [🔗]
Motivation
Experimental determination of 3D protein structures from sequences is usually expensive and time consuming (X-ray crystallography, nuclear magnetic resonance).
Assigning proteins to their respective families allows researchers to infer the shape (and therefore the function) of proteins based only on shared features and evolutionary relationships.
Objective
Description
The goal is to develop a predictive model capable of classifying protein sequences into the eight most common families in the UniProt database, designated as Reviewed/Swiss-Prot.
Limitations: We will restrict ourselves to proteins of at most 1000 amino acids in length and those that have evidence of existence.
Data
The dataset uniprotkb.tsv comes from the UniProt Knowledgebase (UniProtKB). The file consists of a subset of UniProtKB/Swiss-Prot, which contains manually annotated records.
[🔗]
Due to the size of the original file, columns that were too large or irrelevant to the task were discarded during the data preprocessing.
import itertools
import pandas as pd
import numpy as np
import missingno as msno
import matplotlib.pyplot as plt
import dtreeviz
from collections import defaultdict
from collections import Counter
from Bio.SeqUtils import IUPACData
from faiss import IndexFlatL2
from sklearn.model_selection import train_test_split
from matplotlib.ticker import MaxNLocator
from sklearn.model_selection import ParameterGrid
from sklearn.base import BaseEstimator
from sklearn.base import ClassifierMixin
from sklearn.utils.validation import check_X_y
from sklearn.utils.validation import check_array
from sklearn.utils.validation import check_is_fitted
from sklearn.utils.multiclass import unique_labels
from sklearn.tree import DecisionTreeClassifier
from sklearn.tree import plot_tree
from sklearn.ensemble import RandomForestClassifier
from sklearn.metrics import accuracy_score
from sklearn.metrics import balanced_accuracy_score
from sklearn.metrics import ConfusionMatrixDisplay
from sklearn.metrics import f1_score
from sklearn.metrics import precision_recall_curve
from sklearn.metrics import classification_report
from sklearn.metrics import RocCurveDisplay
from sklearn.metrics import PrecisionRecallDisplay
from sklearn.decomposition import PCA
from sklearn.feature_extraction.text import TfidfVectorizer
np.random.seed(42)
plt.style.use('ggplot')
red = np.array((226, 74, 51))/255
blue = np.array((52, 138, 189))/255
blue2 = np.array((0, 150, 240))/255
grey = np.array((100, 100, 100))/255
cobalt = np.array((0, 71, 171))/255
knn_color = np.array((192, 64, 0))/255
tree_color = np.array((24, 168, 27))/255
forest_color = np.array((146, 55, 188))/255
main_color = blue2
Dataset
raw_data = pd.read_csv('uniprotkb.tsv', sep='\t', index_col=0)
Overview
The dataset has the following features:
| Feature | Description | |
|---|---|---|
| Entry Name | Unique identifier for a UniProtKB entry | 🔗 |
| Protein names | Name(s) and taxonomy | 🔗 |
| Gene Names | Gene(s) that code the protein sequence | 🔗 |
| Organism | Name(s) of the organism that is the source of the protein | 🔗 |
| Protein existence | Type of evidence that supports the existence of the protein | 🔗 |
| AlphaFoldDB | ID of the structural prediction from AlphaFold database | 🔗 |
| Pfam | Protein family classification of the protein | 🔗 |
| SUPFAM | Superfamily to which the protein belongs | 🔗 |
| Length | Number of amino acids in the canonical sequence | 🔗 |
| Sequence | Canonical protein sequence (primary structure) | 🔗 |
pd.DataFrame([raw_data.count(), raw_data.nunique(), raw_data.dtypes],
index=['Non-Null Count', 'Unique Values', 'Dtype']).T
| Non-Null Count | Unique Values | Dtype | |
|---|---|---|---|
| Entry Name | 570420 | 570420 | object |
| Protein names | 570420 | 166782 | object |
| Gene Names | 545939 | 493775 | object |
| Organism | 570420 | 14534 | object |
| Protein existence | 570420 | 5 | object |
| AlphaFoldDB | 546366 | 546366 | object |
| Pfam | 539105 | 20623 | object |
| SUPFAM | 459110 | 5587 | object |
| Length | 570420 | 3456 | int64 |
| Sequence | 570420 | 482285 | object |
Necessary pre-processing
Some features are inappropriately represented by a list of values.
raw_data.iloc[[10, 42]].T
| Entry | A0A061AE05 | A0A087X1C5 |
|---|---|---|
| Entry Name | PAPSH_CAEEL | CP2D7_HUMAN |
| Protein names | Bifunctional 3'-phosphoadenosine 5'-phosphosul... | Putative cytochrome P450 2D7 (EC 1.14.14.1) |
| Gene Names | pps-1 T14G10.1 | CYP2D7 |
| Organism | Caenorhabditis elegans | Homo sapiens (Human) |
| Protein existence | Evidence at protein level | Uncertain |
| AlphaFoldDB | A0A061AE05; | A0A087X1C5; |
| Pfam | PF01583;PF01747;PF14306; | PF00067; |
| SUPFAM | SSF52374;SSF52540;SSF88697; | SSF48264; |
| Length | 654 | 515 |
| Sequence | MLTPRDENNEGDAMPMLKKPRYSSLSGQSTNITYQEHTISREERAA... | MGLEALVPLAMIVAIFLLLVDLMHRHQRWAARYPPGPLPLPGLGNL... |
The provided sample shows that the representation of the AlphaFoldDB, Pfam and SUPFAM features need to be modified.
data = raw_data.copy()
for col in ['AlphaFoldDB', 'Pfam', 'SUPFAM']:
data[col] = data[col].str.strip(';')
data[col] = data[col].str.split(';')
data[col] = data[col].apply(lambda l: l if isinstance(l, list) else [])
data.iloc[[10, 42]].T
| Entry | A0A061AE05 | A0A087X1C5 |
|---|---|---|
| Entry Name | PAPSH_CAEEL | CP2D7_HUMAN |
| Protein names | Bifunctional 3'-phosphoadenosine 5'-phosphosul... | Putative cytochrome P450 2D7 (EC 1.14.14.1) |
| Gene Names | pps-1 T14G10.1 | CYP2D7 |
| Organism | Caenorhabditis elegans | Homo sapiens (Human) |
| Protein existence | Evidence at protein level | Uncertain |
| AlphaFoldDB | [A0A061AE05] | [A0A087X1C5] |
| Pfam | [PF01583, PF01747, PF14306] | [PF00067] |
| SUPFAM | [SSF52374, SSF52540, SSF88697] | [SSF48264] |
| Length | 654 | 515 |
| Sequence | MLTPRDENNEGDAMPMLKKPRYSSLSGQSTNITYQEHTISREERAA... | MGLEALVPLAMIVAIFLLLVDLMHRHQRWAARYPPGPLPLPGLGNL... |
Exploratory data analysis
In the training phase of the classification model, only the Sequence feature is used to predict the target variable Pfam. Other features will be used to filter out unreliable or irrelevant entries.
Missing values
fig, axes = plt.subplots(2, 1, figsize=(12, 6), layout='constrained', sharex=True, height_ratios=[1, 2])
fig.suptitle('Missing values', fontsize=20)
ax = axes[0]
msno.matrix(raw_data, fontsize=14, sparkline=False, ax=ax, color=main_color)
ax.get_yaxis().set_visible(False)
ax = axes[1]
missings = raw_data.isna().sum()
miss_ticks = missings[(missings > 0) & (missings != 24054)]
bars = ax.bar(missings.index, missings, color=main_color)
ax.set_ylabel('Count', fontsize=14)
ax.tick_params(axis='y', which='major', labelsize=12)
ax.tick_params(axis='x', which='major', labelsize=12, rotation=-15)
for bar, count in zip(bars, missings):
if count < 100:
ax.text(bar.get_x() + bar.get_width()/2, bar.get_y() + 2000, f'{count}', ha='center', fontsize=12)
ax.set_yticks([0, *miss_ticks])
plt.show()
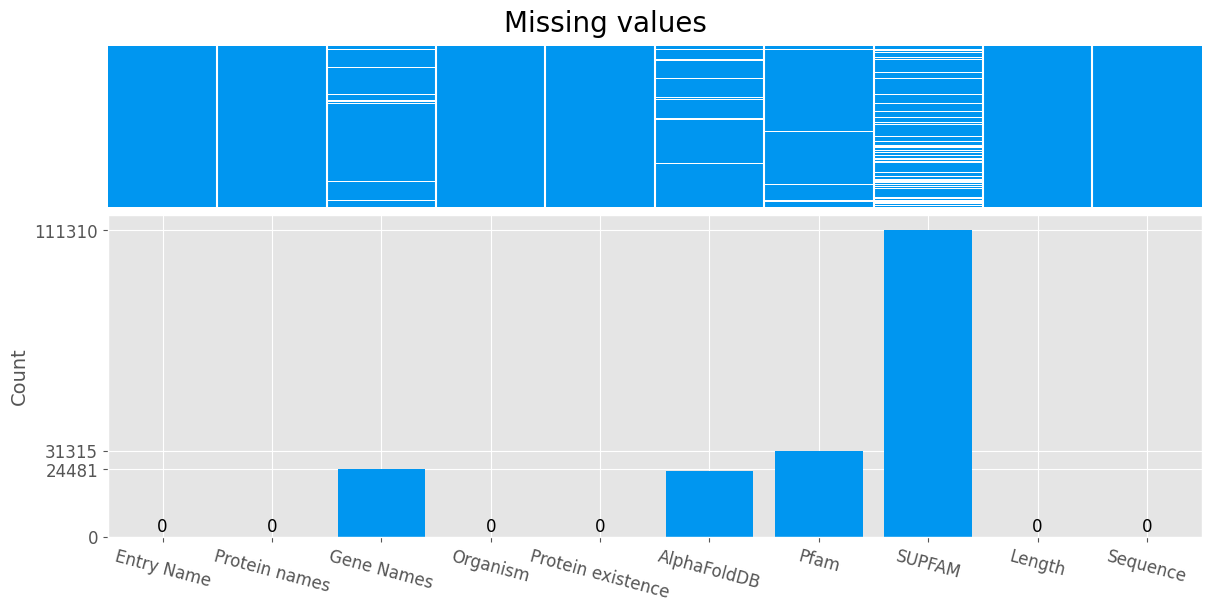
Some entries in the database are missing the Pfam feature. These records will be omitted.
Protein existance
| Type of evidence | Description |
|---|---|
| Protein uncertain | Uncertainty regarding the protein’s existence. |
| Protein predicted | No direct evidence for the protein’s existence at any level (protein, transcript, or homology). |
| Protein inferred by homology | Likely existence of the protein due to the presence of clear orthologs in related species. |
| Experimental evidence at transcript level | Evidence suggests the protein exists based on expression data for its transcript. |
| Experimental evidence at protein level | Clear experimental proof of the protein’s existence. |
existence = data['Protein existence'].value_counts().sort_values()
fig, ax = plt.subplots(1, 1, figsize=(12, 4), layout='constrained')
fig.suptitle('Protein existence', fontsize=20)
bars = ax.barh(existence.index, existence, color=main_color)
ax.set_xlabel('Count', fontsize=14)
ax.tick_params(axis='both', which='major', labelsize=12)
for bar, count in zip(bars, existence):
ax.text(bar.get_width() + ax.get_xlim()[1]*0.005, bar.get_y() + bar.get_height() / 2, f'{count}', va='center', fontsize=12)
ax.set_xlim(0, 430000)
plt.show()
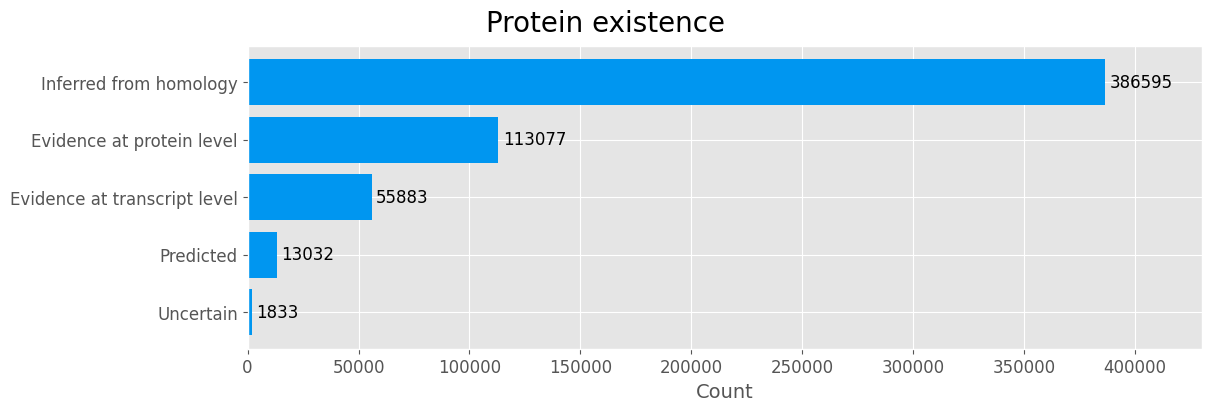
Proteins in the categories Protein predicted and Protein uncertain are removed due to the lack of evidence.
Sequence length
fig, ax = plt.subplots(1, 1, figsize=(12, 3), layout='constrained')
fig.suptitle('Sequence length (all)', size=20)
medianprops = dict(linewidth=2.5, color=main_color)
flierprops = dict(marker='o', markerfacecolor='none', markersize=7, markeredgecolor=main_color)
ax.boxplot(data['Length'], vert=False, widths=[0.4], showfliers=True, flierprops=flierprops, medianprops=medianprops)
ax.tick_params(axis='both', which='major', labelsize=12)
ax.get_yaxis().set_visible(False)
ax.set_xlabel('Length', size=14)
plt.show()
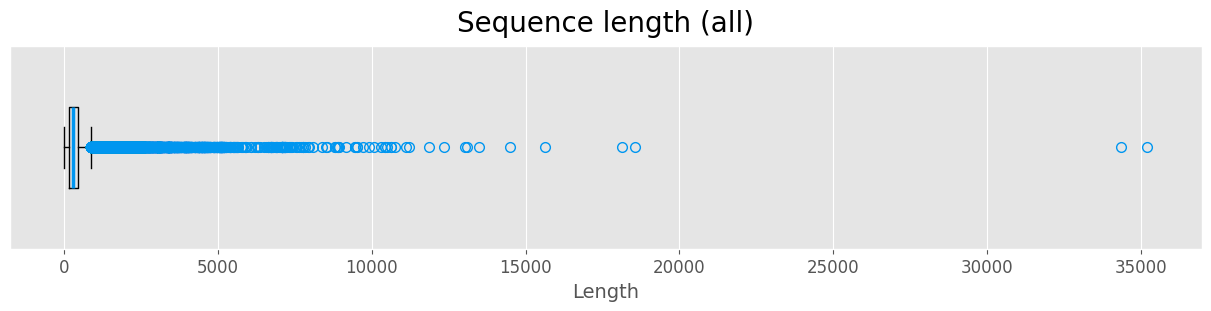
Most of the sequences in the dataset are less than 1000 long. We treat proteins with significantly longer sequences as outliers.
Example of a long protein sequence
data.loc[['Q9H195']].T
| Entry | Q9H195 |
|---|---|
| Entry Name | MUC3B_HUMAN |
| Protein names | Mucin-3B (MUC-3B) (Intestinal mucin-3B) |
| Gene Names | MUC3B |
| Organism | Homo sapiens (Human) |
| Protein existence | Evidence at transcript level |
| AlphaFoldDB | [Q9H195] |
| Pfam | [] |
| SUPFAM | [SSF82671] |
| Length | 13477 |
| Sequence | MQLLGLLSILWMLKSSPGATGTLSTATSTSHVTFPRAEATRTALSN... |

Proteins with sequence longer than 1000 will be removed from the dataset to reduce computational overhead.
Distribution of sequence lengths
flengths = data.loc[data['Length'] < 1000, ['Length']]
fig, axes = plt.subplots(2, 1, figsize=(12, 6), sharex=True, layout='constrained')
fig.suptitle('Sequence length (< 1000)', size=20)
flengths = data.loc[data['Length'] < 1000, ['Length']]
ax = axes[0]
ax.hist(flengths, bins=40, color=main_color)
ax.set_ylabel('Count', size=14)
ax.tick_params(labelbottom=False, labelsize=12)
ax.tick_params(axis='x', which='both', length=0)
medianprops = dict(linewidth=2.5, color=main_color)
flierprops = dict(marker='o', markerfacecolor='none', markersize=7, markeredgecolor=main_color, alpha=0.002)
ax = axes[1]
ax.boxplot(flengths, vert=False, widths=[0.4], showfliers=True, flierprops=flierprops, medianprops=medianprops)
ax.get_yaxis().set_visible(False)
ax.tick_params(axis='both', which='major', labelsize=12)
ax.set_xlabel('Length', size=14)
ax.set_xticks(list(ax.get_xticks()) + [np.median(flengths)])
plt.show()
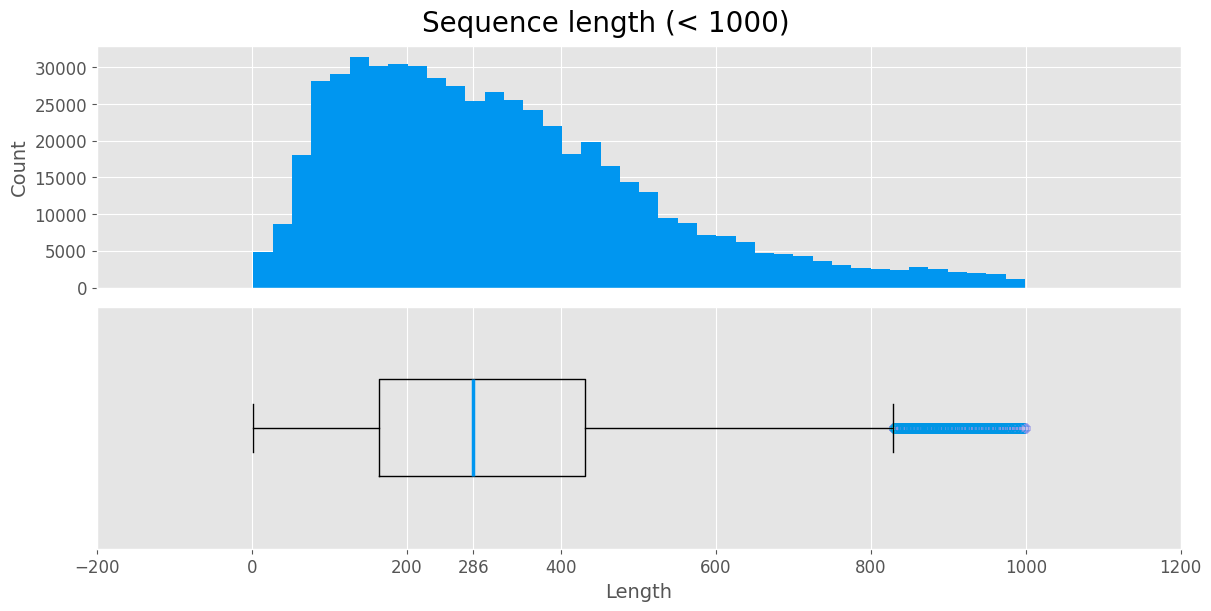
The sequence length histogram has a log-normal distribution, which is commonly observed in proteins.
Organism
organism = data['Organism'].value_counts().sort_values().tail(5)
organism = organism.rename({
"Saccharomyces cerevisiae (strain ATCC 204508 / S288c) (Baker's yeast)" : "Saccharomyces cerevisiae (Baker's yeast)"
})
fig, ax = plt.subplots(1, 1, figsize=(12, 4), layout='constrained')
fig.suptitle('Most frequent organisms in Swiss-Prot', fontsize=20)
bars = ax.barh(organism.index, organism, color=main_color)
ax.set_xlabel('Count', fontsize=14)
ax.tick_params(axis='both', which='major', labelsize=12)
ax.set_xticks([0, *organism[:3], *organism[4:]])
plt.show()
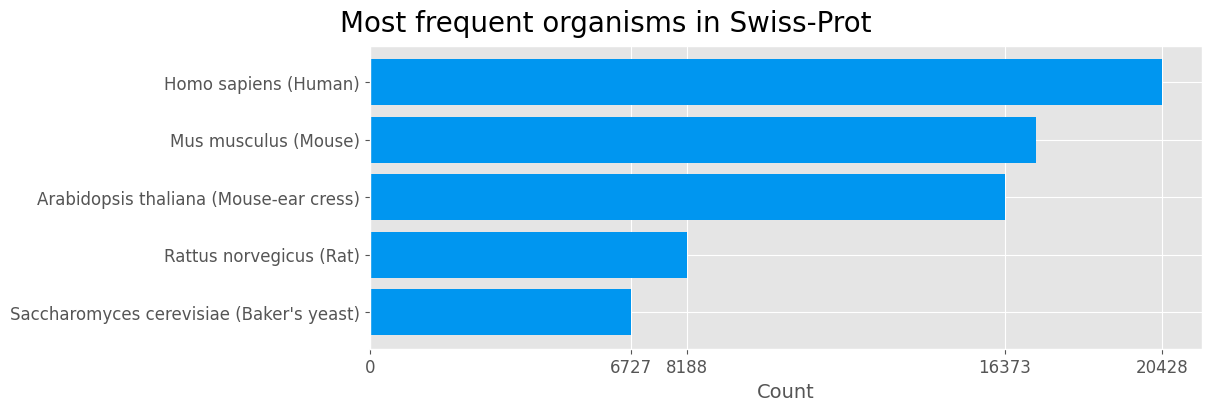
| Human | Mouse | Mouse-ear cress | Rat | Baker’s yeast |
|---|---|---|---|---|
 |  |  |  |  |
Protein family
fam_count = defaultdict(int)
for row in data['Pfam'].to_numpy():
for el in row:
fam_count[el] += 1
fams = pd.Series(dict(fam_count))
top_fams = fams.sort_values(ascending=True).tail(8)
fig, ax = plt.subplots(1, 1, figsize=(12, 4), layout='constrained')
fig.suptitle('8 most frequent protein families', fontsize=20)
bars = ax.barh(top_fams.index, top_fams, color=main_color)
ax.set_xlabel('Count', fontsize=14)
ax.tick_params(axis='both', which='major', labelsize=12)
plt.show()
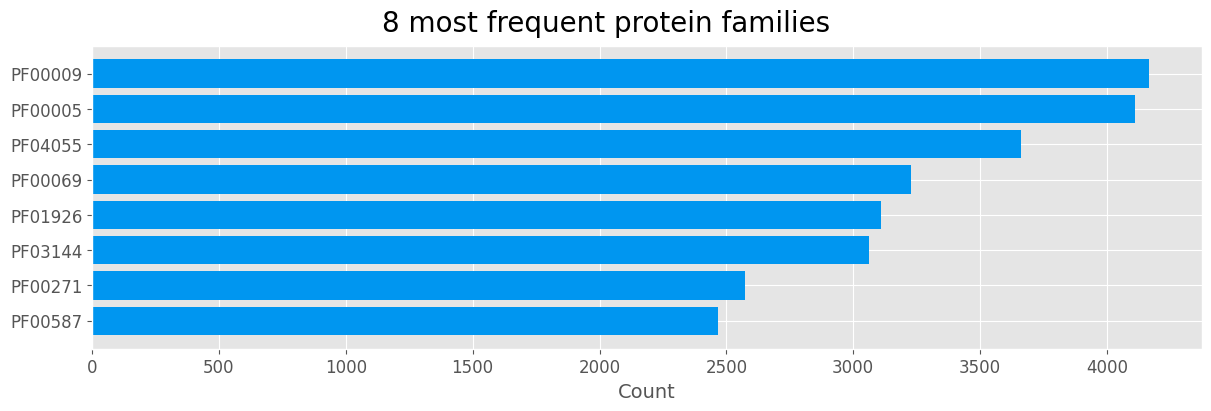
| Protein family | Domain name | |
|---|---|---|
| PF00009 | Elongation factor Tu GTP binding domain | 🔗 |
| PF00005 | ABC transporter | 🔗 |
| PF04055 | Radical SAM superfamily | 🔗 |
| PF00069 | Protein kinase domain | 🔗 |
| PF01926 | 50S ribosome-binding GTPase | 🔗 |
| PF03144 | Elongation factor Tu domain 2 | 🔗 |
| PF00271 | Helicase conserved C-terminal domain | 🔗 |
| PF00587 | tRNA synthetase class II core domain | 🔗 |
Amino acid sequence
one2all = {'A': ('A', 'ALA', 'alanine'), 'R': ('R', 'ARG', 'arginine'), 'N': ('N', 'ASN', 'asparagine'), 'D': ('D', 'ASP', 'aspartic acid'),
'C': ('C', 'CYS', 'cysteine'), 'Q': ('Q', 'GLN', 'glutamine'), 'E': ('E', 'GLU', 'glutamic acid'), 'G': ('G', 'GLY', 'glycine'),
'H': ('H', 'HIS', 'histidine'), 'I': ('I', 'ILE', 'isoleucine'), 'L': ('L', 'LEU', 'leucine'), 'K': ('K', 'LYS', 'lysine'),
'M': ('M', 'MET', 'methionine'), 'F': ('F', 'PHE', 'phenylalanine'), 'P': ('P', 'PRO', 'proline'), 'S': ('S', 'SER', 'serine'),
'T': ('T', 'THR', 'threonine'), 'W': ('W', 'TRP', 'tryptophan'), 'Y': ('Y', 'TYR', 'tyrosine'), 'V': ('V', 'VAL', 'valine'),
'X': ('X', 'GLX', 'glutaminx'), 'Z': ('Z', 'GLI', 'glycine'), 'J': ('J', 'NLE', 'norleucine'), 'U': ('U', 'CYC', 'cysteinc'),
'O': ('O', 'PYL', 'pyrrolysine'), 'B': ('B', 'ASX', 'asparagine')}
counter = Counter()
for seq in data['Sequence']:
counter.update(set(seq))
acids = pd.DataFrame(counter.keys(), columns=['Letter'])
acids['Code'] = acids['Letter'].apply(lambda l: one2all[l][1])
acids['Name'] = acids['Letter'].apply(lambda l: one2all[l][2])
acids['Total count'] = counter.values()
acids['Relative count'] = acids['Total count'] / acids['Total count'].sum()
acids.style.hide()
| Letter | Code | Name | Total count | Relative count |
|---|---|---|---|---|
| P | PRO | proline | 561293 | 0.050865 |
| H | HIS | histidine | 538618 | 0.048810 |
| Y | TYR | tyrosine | 550058 | 0.049847 |
| K | LYS | lysine | 563402 | 0.051056 |
| F | PHE | phenylalanine | 559457 | 0.050698 |
| N | ASN | asparagine | 560037 | 0.050751 |
| M | MET | methionine | 564368 | 0.051143 |
| E | GLU | glutamic acid | 561780 | 0.050909 |
| T | THR | threonine | 564617 | 0.051166 |
| V | VAL | valine | 566679 | 0.051353 |
| D | ASP | aspartic acid | 560915 | 0.050831 |
| R | ARG | arginine | 564233 | 0.051131 |
| Q | GLN | glutamine | 557412 | 0.050513 |
| W | TRP | tryptophan | 454108 | 0.041152 |
| S | SER | serine | 566731 | 0.051358 |
| L | LEU | leucine | 567243 | 0.051404 |
| G | GLY | glycine | 567343 | 0.051413 |
| A | ALA | alanine | 566448 | 0.051332 |
| I | ILE | isoleucine | 564607 | 0.051165 |
| C | CYS | cysteine | 472913 | 0.042856 |
| X | GLX | glutaminx | 2263 | 0.000205 |
| U | CYC | cysteinc | 254 | 0.000023 |
| Z | GLI | glycine | 87 | 0.000008 |
| B | ASX | asparagine | 113 | 0.000010 |
| O | PYL | pyrrolysine | 29 | 0.000003 |
Note that, in addition to the standard set of 20 amino acids, there are 5 other amino acids that are non-standard (and quite rare).
Data pre-processing
Data filtering based on EDA findings
We will not consider proteins belonging to multiple families or domains to ensure unambiguity of training and evaluation. In addition, proteins that have insufficient evidence of existence or are composed of chain lengths exceeding 1000 are also removed. The reasons are discussed in the EDA.
datac = data.copy()
datac = datac[datac['Pfam'].str.len() == 1]
datac['Pfam'] = datac['Pfam'].str[0]
datac = datac[datac['Protein existence'].isin(['Evidence at protein level', 'Evidence at transcript level', 'Inferred from homology'])]
datac = datac[datac['Length'] <= 1000]
We also filter the data belonging to the prority protein families. We extend them with sequences from unspecified classes so that the trained model can also determine whether or not a sequence belongs to the selected families.
top_fams = datac['Pfam'].value_counts()
top_fams = top_fams.sort_values(ascending=False).head(8)
intop_df = datac[datac['Pfam'].isin(top_fams.index)].copy()
other_df = datac[~datac['Pfam'].isin(top_fams.index)].copy()
indexes = other_df.sample(int(top_fams.max() * 1)).index.tolist()
indexes.extend(intop_df.index)
dataset = datac.loc[indexes]
We apply all these filters before splitting them into training and test sets to meet the objectives specified in the problem statement.
Remapping the target variable
pfam_cat = pd.CategoricalDtype([*top_fams.index, 'OTHER'], ordered=False)
dataset['Pfam'] = dataset['Pfam'].apply(lambda fam: fam if fam in top_fams else 'OTHER')
dataset['Pfam'] = dataset['Pfam'].astype(pfam_cat)
filtered_fams = dataset['Pfam'].value_counts()
fig, ax = plt.subplots(1, 1, figsize=(12, 4), layout='constrained')
fig.suptitle('Filtered protein families', fontsize=20)
bars = ax.barh(filtered_fams.index, filtered_fams, color=main_color)
ax.set_xlabel('Count', fontsize=16)
ax.tick_params(axis='both', which='major', labelsize=14)
ax.invert_yaxis()
plt.show()
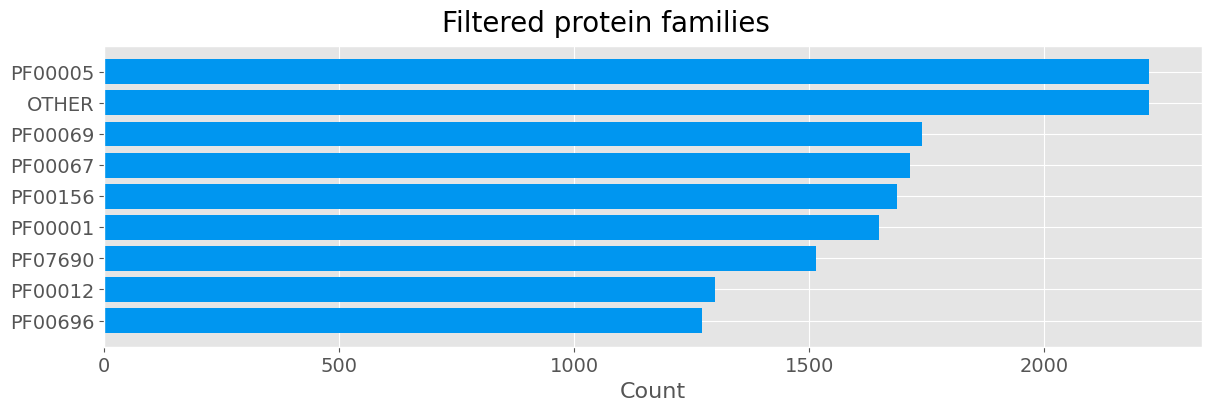
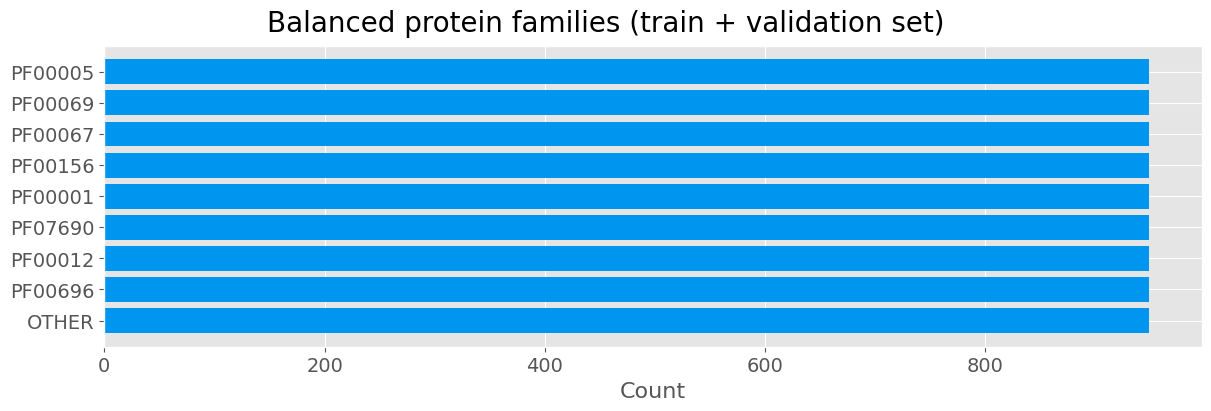
The filtered dataset has been suitably remapped. On the new data we observe an imbalance in the classes represented, specifically class PF00005 is represented twice as much as PF00012 or PF00696. We will address this issue by undersampling.
Train-validation-test split
X_all = dataset['Sequence']
y_all = dataset['Pfam']
X_train_val, X_test, y_train_val, y_test = train_test_split(X_all, y_all, test_size=0.24)
Undersampling unbalanced training data
We now perform undersampling of the training data so that the training respects class imbalance issue. We apply it after putting the test set aside so that the integrity of the test set is not compromised.
indices = []
min_count = y_train_val.value_counts().min()
for fam in y_train_val.unique():
fam_indices = y_train_val.loc[y_train_val == fam].index
sample_indices = np.random.choice(fam_indices, min_count, replace=False)
indices.extend(sample_indices)
y_train_val = y_train_val.loc[indices]
X_train_val = X_train_val.loc[indices]
X_train, X_val, y_train, y_val = train_test_split(X_train_val, y_train_val, test_size=0.36)
filtered_fams = y_train_val.value_counts()
fig, ax = plt.subplots(1, 1, figsize=(12, 4), layout='constrained')
fig.suptitle('Balanced protein families (train + validation set)', fontsize=20)
bars = ax.barh(filtered_fams.index, filtered_fams, color=main_color)
ax.set_xlabel('Count', fontsize=16)
ax.tick_params(axis='both', which='major', labelsize=14)
ax.invert_yaxis()
plt.show()
split_df = pd.DataFrame([X_train.shape[0], X_val.shape[0], X_test.shape[0]], index=['Train', 'Validation', 'Test'], columns=['Size'])
split_df['Relative size'] = split_df['Size'] / split_df['Size'].sum()
split_df['Relative size'] = split_df['Relative size'].round(2)
split_df
| Size | Relative size | |
|---|---|---|
| Train | 5466 | 0.45 |
| Validation | 3075 | 0.25 |
| Test | 3678 | 0.30 |
Sequence embedding
Now we convert the protein sequences into numerical vectors. This is done using TF-IDF embedding.
pd.DataFrame([X_train, y_train]).T.head()
| Sequence | Pfam | |
|---|---|---|
| Entry | ||
| S7Z6X4 | MLVQYQNLPVQNIPVLLLSCGFLAILFRSLVLRVRYYRKAQAWGCK... | PF00067 |
| Q9Y5N1 | MERAPPDGPLNASGALAGEAAAAGGARGFSAAWTAVLAALMALLIV... | PF00001 |
| P39583 | MDLSVTHMDDLKTVMEDWKNELLVYKFALDALDTKFSIISQEYNLI... | OTHER |
| Q9R0M1 | MESSTAFYDYHDKLSLLCENNVIFFSTISTIVLYSLVFLLSLVGNS... | PF00001 |
| Q9A076 | MTLASQIATQLLDIKAVYLKPEDPFTWASGIKSPIYTDNRVTLSYP... | PF00156 |
TF-IDF
Wikipedia [🔗]:
The term frequency–inverse document frequency is a measure of a word’s importance to a document within a collection.
\[ \text{tf}(t,d) = \frac{f_{t,d}}{\sum_{t' \in d} f_{t',d}} \]\[ \text{idf}(t,\mathcal{D}) = \log \left( {\frac{|\mathcal{D}|}{|\{ d \in \mathcal{D} \mid t \in d \}|}} \right) \]
- term frequency \(\text{tf}(t,d)\) is the relative frequency of term \(t\) within document \(d\), and
- inverse document frequency \(\text{idf}(t,\mathcal{D})\) is the logarithmically scaled inverse fraction of the documents \(\mathcal{D}\) that contain the term \(t\).
Tf–idf is calculated as \(\text{tf}(t,d) \cdot \text{idf}(t,\mathcal{D})\).
In our context, the “word” represents an individual amino acid, the “document” represents the corresponding protein sequence and the “collection” represents all available proteins in the training set.
N-gram
Wikipedia [🔗]:
An N-gram is a contiguous sequence of N items, such as words or characters, extracted from a text or speech. N-grams are commonly used in language modeling and statistical analysis to capture patterns and dependencies within a given dataset.
In our task, the “items” are amino acids.
Vectorizer
Below are some examples of n-grams of amino acids.
def get_vectorizer(X, ngram_range):
vectorizer = TfidfVectorizer(strip_accents='ascii', lowercase=False, analyzer='char', ngram_range=ngram_range)
vectorizer.fit(X)
return vectorizer
uni = get_vectorizer(X_train, (1, 1))
bi = get_vectorizer(X_train, (2, 2))
tri = get_vectorizer(X_train, (3, 3))
vect_dict = {}
for label, vectorizer in zip(['uni', 'bi', 'tri'], [uni, bi, tri]):
vect_dict[label] = {
'train': {'X': np.asarray(vectorizer.transform(X_train).todense()),
'y': y_train.cat.codes.to_numpy()},
'val': {'X': np.asarray(vectorizer.transform(X_val).todense()),
'y': y_val.cat.codes.to_numpy()},
'test': {'X': np.asarray(vectorizer.transform(X_test).todense()),
'y': y_test.cat.codes.to_numpy()},
}
pd.DataFrame.from_dict({
'unigram_vectorizer': uni.get_feature_names_out()[:19],
'bigram_vectorizer': bi.get_feature_names_out()[:19],
'trigram_vectorizer': tri.get_feature_names_out()[:19],
}).T.rename(columns={i:'' for i in range(19)})
| unigram_vectorizer | A | C | D | E | F | G | H | I | K | L | M | N | P | Q | R | S | T | V | W |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| bigram_vectorizer | AA | AC | AD | AE | AF | AG | AH | AI | AK | AL | AM | AN | AP | AQ | AR | AS | AT | AV | AW |
| trigram_vectorizer | AAA | AAC | AAD | AAE | AAF | AAG | AAH | AAI | AAK | AAL | AAM | AAN | AAP | AAQ | AAR | AAS | AAT | AAV | AAW |
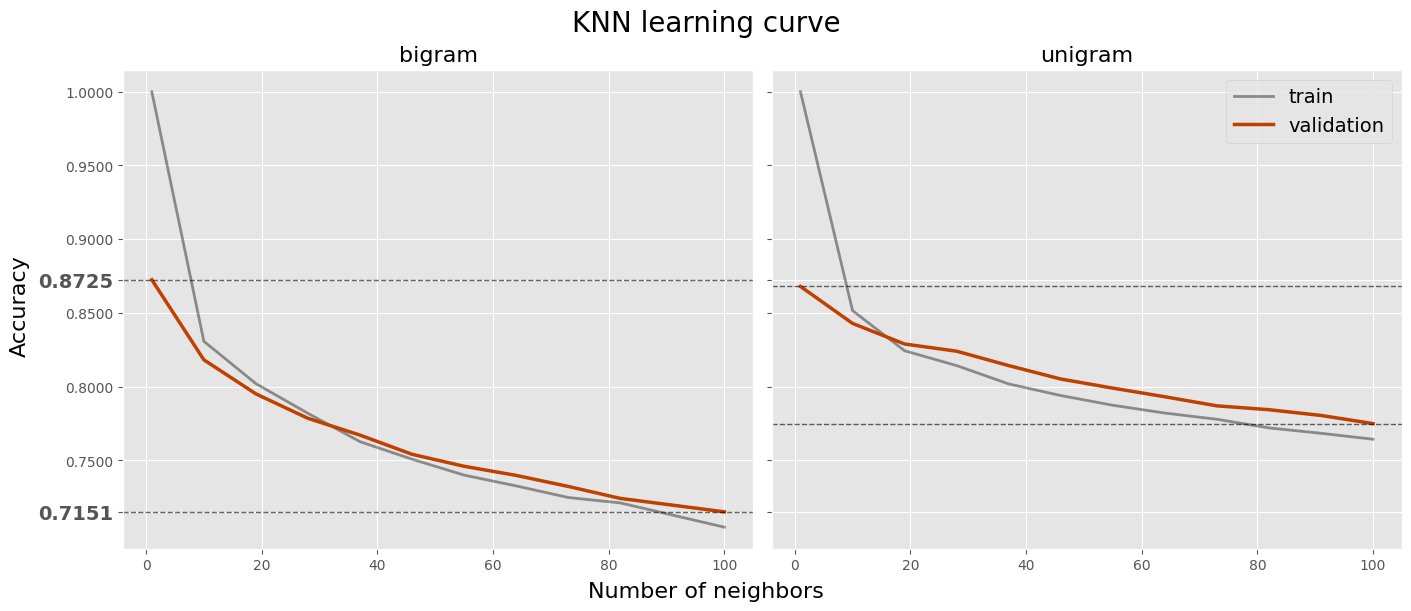
Due to the higher computational cost, we will limit the training to unigrams and bigrams.
Example of a vectorization
matrix = uni.transform([data.loc['P62547', 'Sequence']])
display(pd.DataFrame(data.loc['P62547', [
'Entry Name', 'Organism', 'Protein existence', 'Pfam', 'Length', 'Sequence'
]]).T)
print(matrix.toarray()[0].round(2).tolist())
| Entry Name | Organism | Protein existence | Pfam | Length | Sequence | |
|---|---|---|---|---|---|---|
| P62547 | CR16_RANCH | Ranoidea chloris (Red-eyed tree frog) (Litoria... | Evidence at protein level | [PF07440] | 25 | GLFSVLGAVAKHVLPHVVPVIAEKL |
[0.33, 0.0, 0.0, 0.11, 0.11, 0.22, 0.22, 0.11, 0.22, 0.44, 0.0, 0.0, 0.22, 0.0, 0.0, 0.11, 0.0, 0.67, 0.0, 0.0, 0.0]
| Sequence | Vectorizer | Unigram vector | |
|---|---|---|---|
 | GLFSVLGAVAKHVLPHVVPVIAEKL | ─────────➤ | [0.33, 0.0, 0.0, 0.11, 0.11, 0.22, 0.23, 0.11, 0.22, 0.44, 0.0, 0.0, 0.0, 0.22, 0.0, 0.0, 0.11, 0.0, 0.0, 0.67, 0.0, 0.0, 0.0] |
Model training
We will train and compare the performance of three models:
- 🟠 k-nearest neighbors,
- 🟢 decision tree,
- 🟣 random forest.
When comparing different models, we will primarily consider accuracy.
\[ \text{Accuracy} = \frac{\#\text{correct classifications}}{\#\text{all classifications}} = \frac{1}{N} \sum_{i=1}^{N} \mathbb{1}_{\{\hat{y}_i = y_i\}} \]Other metrics we will use for evaluation are precision, recall and F1 score.
| Precision \(P\) | Recall \(R\) | \(F_1\) score |
|---|---|---|
| \[ \frac{TP}{TP + FP} \] | \[ \frac{TP}{TP + FN} \] | \[ 2 \frac{P_{i} \cdot R_{i}}{P_{i} + R_{i}} \] |
K-nearest neighbours
Custom implementation with faiss library
We implement a custom algorithm using the faiss library, which provides an interface for a more efficient kNN.
class KNeighborsClassifier(BaseEstimator, ClassifierMixin):
def __init__(self, k=5):
self.index = None
self.y = None
self.k = k
def fit(self, X, y):
X, y = check_X_y(X, y)
self.classes_ = unique_labels(y)
self.index = IndexFlatL2(X.shape[1])
self.index.add(X.astype(np.float32))
self.y = y
def predict(self, X):
check_is_fitted(self)
X = check_array(X)
distances, indices = self.index.search(X.astype(np.float32), k=self.k)
votes = self.y[indices]
predictions = np.array([np.argmax(np.bincount(x)) for x in votes])
return predictions
Hyperparameter tunning
| Hyperparameter | Description |
|---|---|
| n_neighbors | Number of nearest neighbours |
| ngram | Configuration of n-gram vectorizer |
param_grid = ParameterGrid({
'n_neighbors': range(1, 101, 9),
'ngram': ['uni', 'bi'],
})
log_knn = pd.DataFrame(columns=['n_neighbors', 'ngram', 'train_accuracy', 'val_accuracy'])
estimators_knn = []
for params in param_grid:
train_ngram = vect_dict[params['ngram']]['train']
val_ngram = vect_dict[params['ngram']]['val']
clf = KNeighborsClassifier(k=params['n_neighbors'])
clf.fit(train_ngram['X'], train_ngram['y'])
train_accuracy = accuracy_score(train_ngram['y'], clf.predict(train_ngram['X']))
val_accuracy = accuracy_score(val_ngram['y'], clf.predict(val_ngram['X']))
log_knn.loc[len(log_knn.index)] = [params['n_neighbors'], params['ngram'], train_accuracy, val_accuracy]
estimators_knn.append(clf)
top_knns = log_knn.sort_values('val_accuracy', ascending=False)
best_knn = estimators_knn[top_knns.index[0]]
h = top_knns.head(10)
h.index = np.arange(1, len(h)+1)
h
| n_neighbors | ngram | train_accuracy | val_accuracy | |
|---|---|---|---|---|
| 1 | 1 | bi | 1.000000 | 0.872520 |
| 2 | 1 | uni | 1.000000 | 0.867967 |
| 3 | 10 | uni | 0.851628 | 0.842927 |
| 4 | 19 | uni | 0.824369 | 0.828943 |
| 5 | 28 | uni | 0.814307 | 0.824065 |
| 6 | 10 | bi | 0.830772 | 0.818211 |
| 7 | 37 | uni | 0.801866 | 0.814309 |
| 8 | 46 | uni | 0.793999 | 0.805203 |
| 9 | 55 | uni | 0.787413 | 0.799024 |
| 10 | 19 | bi | 0.802049 | 0.795122 |
log_knn.sort_index(inplace=True)
halpha = 0.6
# fig, axes = plt.subplots(1, 3, figsize=(14, 6), layout='constrained', sharey=True)
fig, axes = plt.subplots(1, 2, figsize=(14, 6), layout='constrained', sharey=True)
fig.suptitle('KNN learning curve', size=20)
fig.supxlabel('Number of neighbors', size=16)
fig.supylabel('Accuracy', size=16)
df = log_knn[log_knn['ngram'] == 'bi'].copy()
ax = axes[0]
ax.set_title('bigram', size=16)
ax.plot(df['n_neighbors'], df['train_accuracy'], label='train', color='black', linewidth=2, alpha=0.4)
ax.plot(df['n_neighbors'], df['val_accuracy'], label='validation', color=knn_color, linewidth=2.5)
ax.axhline(df['val_accuracy'].max(), color='black', linestyle='--', linewidth=1, alpha=halpha)
ax.axhline(df['val_accuracy'].min(), color='black', linestyle='--', linewidth=1, alpha=halpha)
bounderies = [df['val_accuracy'].min().round(4), df['val_accuracy'].max().round(4)]
ticks = [i/100 for i in range(75, 101, 5)]
for b in bounderies:
for tick in ticks:
if abs(tick - b) < 0.02:
ticks.remove(tick)
ax.set_yticks(bounderies + ticks)
for i, tick in enumerate(ax.yaxis.get_major_ticks()):
if i in [0, 1]:
tick.label1.set_size(14)
tick.label1.set_weight(1000)
df = log_knn[log_knn['ngram'] == 'uni'].copy()
ax = axes[1]
ax.set_title('unigram', size=16)
ax.plot(df['n_neighbors'], df['train_accuracy'], label='train', color='black', linewidth=2, alpha=0.4)
ax.plot(df['n_neighbors'], df['val_accuracy'], label='validation', color=knn_color, linewidth=2.5)
ax.axhline(df['val_accuracy'].max(), color='black', linestyle='--', linewidth=1, alpha=halpha)
ax.axhline(df['val_accuracy'].min(), color='black', linestyle='--', linewidth=1, alpha=halpha)
# df = log_knn[log_knn['ngram'] == 'uni'].copy()
# ax = axes[2]
# ax.set_title('unigram', size=16)
# ax.plot(df['n_neighbors'], df['train_accuracy'], label='train', color='black', linewidth=2, alpha=0.4)
# ax.plot(df['n_neighbors'], df['val_accuracy'], label='validation', color=knn_color, linewidth=2.5)
# ax.axhline(df['val_accuracy'].max(), color='black', linestyle='--', linewidth=1, alpha=halpha)
ax.legend(loc='upper right', fontsize=14)
plt.show()
Model evaluation
bi_val_vec = vect_dict['bi']['val']
y_true = bi_val_vec['y']
y_hat = best_knn.predict(bi_val_vec['X']).astype(np.int8)
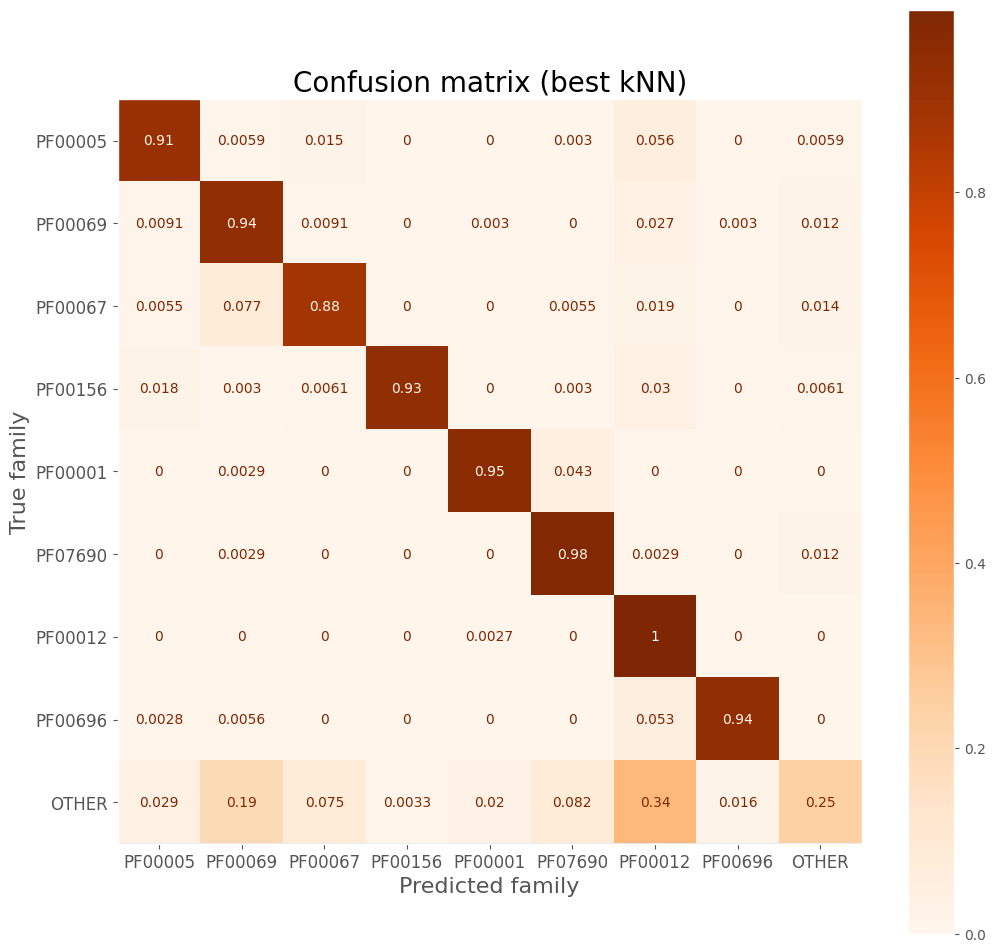
Confusion matrix
disp = ConfusionMatrixDisplay.from_estimator(
best_knn, bi_val_vec['X'], bi_val_vec['y'], cmap=plt.cm.Oranges,
display_labels=pfam_cat.categories, normalize='true'
)
disp.figure_.set_size_inches((12, 12))
ax = disp.ax_
ax.set_title('Confusion matrix (best kNN)', size=20)
ax.set_xlabel('Predicted family', size=16)
ax.set_ylabel('True family', size=16)
ax.tick_params(axis='both', which='major', labelsize=12)
ax.grid(False)
Precision, recall, F1 score
report = classification_report(y_true, y_hat, target_names=pfam_cat.categories, output_dict=True)
pd.DataFrame(report).T.round(2).iloc[:-3]
| precision | recall | f1-score | support | |
|---|---|---|---|---|
| PF00005 | 0.94 | 0.91 | 0.93 | 338.0 |
| PF00069 | 0.77 | 0.94 | 0.84 | 330.0 |
| PF00067 | 0.91 | 0.88 | 0.89 | 362.0 |
| PF00156 | 1.00 | 0.93 | 0.96 | 329.0 |
| PF00001 | 0.98 | 0.95 | 0.96 | 346.0 |
| PF07690 | 0.88 | 0.98 | 0.93 | 341.0 |
| PF00012 | 0.69 | 1.00 | 0.81 | 367.0 |
| PF00696 | 0.98 | 0.94 | 0.96 | 356.0 |
| OTHER | 0.82 | 0.25 | 0.38 | 306.0 |
Best kNN model
| n_neighbors | 1 |
| ngram | bi |
knn_eval = pd.DataFrame([
accuracy_score(y_true, y_hat),
], index=['Accuracy'], columns=['KNN'])
knn_eval
| KNN | |
|---|---|
| Accuracy | 0.87252 |
Decision tree
Hyperparameter tunning
| Hyperparameter | Description |
|---|---|
| max_depth | Maximum depth of the tree |
| criterion | Function to measure the quality of a split |
| ngram | Configuration of n-gram vectorizer |
| Criterion | Formula |
|---|---|
| gini | \[ H(\mathcal{D}) = \sum_{k} p_k \left( 1 - p_k \right) \] |
| entropy | \[ H(\mathcal{D}) = - \sum_{k} p_k \log(p_k) \] |
param_grid = ParameterGrid({
'max_depth': range(1, 32, 6),
'criterion': ['gini', 'entropy'],
'ngram': ['uni', 'bi'],
})
log_tree = pd.DataFrame(columns=['criterion', 'max_depth', 'ngram', 'train_accuracy', 'val_accuracy'])
estimators_tree = []
for params in param_grid:
train_ngram = vect_dict[params['ngram']]['train']
val_ngram = vect_dict[params['ngram']]['val']
clf = DecisionTreeClassifier(criterion=params['criterion'], max_depth=params['max_depth'])
clf.fit(train_ngram['X'], train_ngram['y'])
train_accuracy = accuracy_score(train_ngram['y'], clf.predict(train_ngram['X']))
val_accuracy = accuracy_score(val_ngram['y'], clf.predict(val_ngram['X']))
log_tree.loc[len(log_tree.index)] = [params['criterion'], params['max_depth'], params['ngram'], train_accuracy, val_accuracy]
estimators_tree.append(clf)
top_trees = log_tree.sort_values('val_accuracy', ascending=False)
best_tree = estimators_tree[top_trees.index[0]]
h = top_trees.head(10)
h.index = np.arange(1, len(h)+1)
h
| criterion | max_depth | ngram | train_accuracy | val_accuracy | |
|---|---|---|---|---|---|
| 1 | gini | 25 | uni | 1.000000 | 0.757398 |
| 2 | gini | 13 | uni | 0.977863 | 0.755122 |
| 3 | gini | 19 | uni | 0.998353 | 0.754797 |
| 4 | gini | 31 | uni | 1.000000 | 0.754472 |
| 5 | entropy | 13 | uni | 0.989572 | 0.745691 |
| 6 | entropy | 25 | bi | 1.000000 | 0.743089 |
| 7 | entropy | 25 | uni | 1.000000 | 0.742764 |
| 8 | entropy | 31 | uni | 1.000000 | 0.741789 |
| 9 | entropy | 31 | bi | 1.000000 | 0.741138 |
| 10 | entropy | 19 | bi | 1.000000 | 0.741138 |
log_tree = log_tree[log_tree['criterion'] == 'gini']
log_tree.sort_index(inplace=True)
halpha = 0.5
# fig, axes = plt.subplots(1, 3, figsize=(14, 6), layout='constrained', sharey=True)
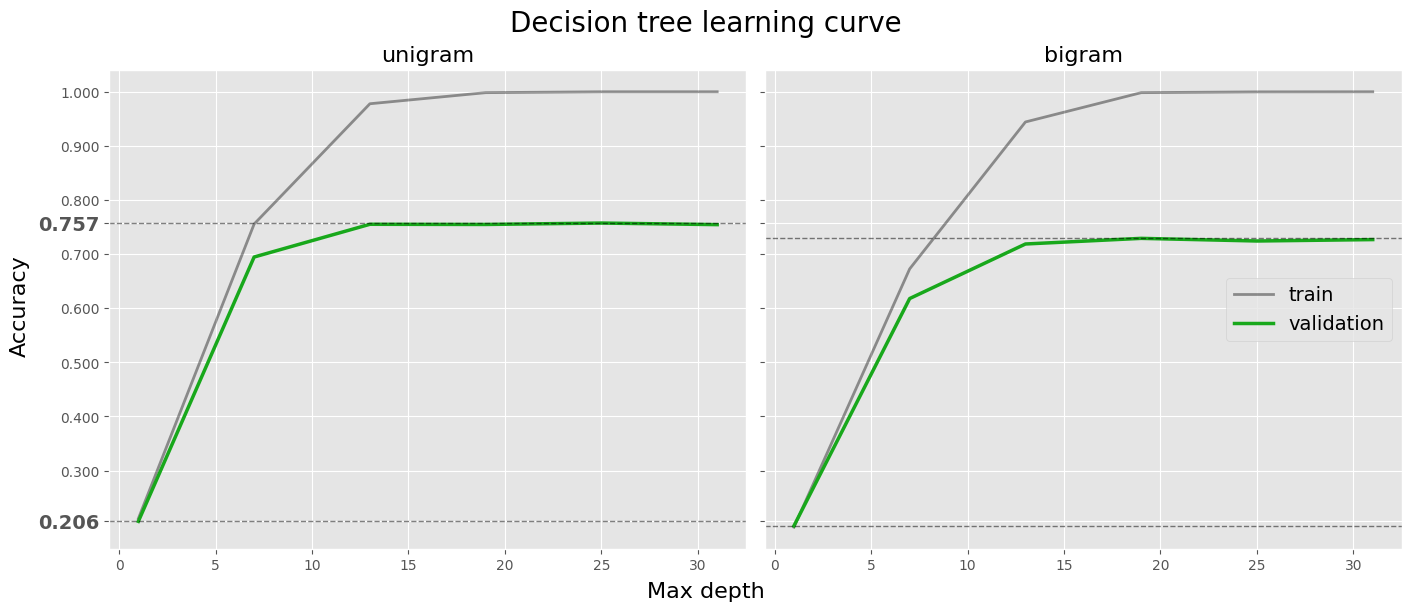
fig, axes = plt.subplots(1, 2, figsize=(14, 6), layout='constrained', sharey=True)
fig.suptitle('Decision tree learning curve', size=20)
fig.supxlabel('Max depth', size=16)
fig.supylabel('Accuracy', size=16)
df = log_tree[log_tree['ngram'] == 'uni'].copy()
ax = axes[0]
ax.set_title('unigram', size=16)
ax.plot(df['max_depth'], df['train_accuracy'], label='train', color='black', linewidth=2, alpha=0.4)
ax.plot(df['max_depth'], df['val_accuracy'], label='validation', color=tree_color, linewidth=2.5)
ax.axhline(df['val_accuracy'].max(), color='black', linestyle='--', linewidth=1, alpha=halpha)
ax.axhline(df['val_accuracy'].min(), color='black', linestyle='--', linewidth=1, alpha=halpha)
bounderies = [df['val_accuracy'].min().round(4), df['val_accuracy'].max().round(4)]
ticks = [i/100 for i in range(0, 101, 10)]
for b in bounderies:
for tick in ticks:
if abs(tick - b) < 0.04:
ticks.remove(tick)
ax.set_yticks(bounderies + ticks)
for i, tick in enumerate(ax.yaxis.get_major_ticks()):
if i in [0, 1]:
tick.label1.set_size(14)
tick.label1.set_weight(1000)
df = log_tree[log_tree['ngram'] == 'bi'].copy()
ax = axes[1]
ax.set_title('bigram', size=16)
ax.plot(df['max_depth'], df['train_accuracy'], label='train', color='black', linewidth=2, alpha=0.4)
ax.plot(df['max_depth'], df['val_accuracy'], label='validation', color=tree_color, linewidth=2.5)
ax.axhline(df['val_accuracy'].max(), color='black', linestyle='--', linewidth=1, alpha=halpha)
ax.axhline(df['val_accuracy'].min(), color='black', linestyle='--', linewidth=1, alpha=halpha)
# df = log_tree[log_tree['ngram'] == 'uni'].copy()
# ax = axes[2]
# ax.set_title('unigram', size=16)
# ax.plot(df['max_depth'], df['train_accuracy'], label='train', color='black', linewidth=2, alpha=0.4)
# ax.plot(df['max_depth'], df['val_accuracy'], label='validation', color=tree_color, linewidth=2.5)
# ax.axhline(df['val_accuracy'].max(), color='black', linestyle='--', linewidth=1, alpha=halpha)
# ax.axhline(df['val_accuracy'].min(), color='black', linestyle='--', linewidth=1, alpha=halpha)
ax.legend(loc='center right', fontsize=14)
plt.show()
Example of a classification using a decision tree
Here, we visualize a decision process for classifying the family of the Chaperone protein DnaK using a decision tree of depth 4. The process is shown in the following diagram.
| Sequence | Vectorizer | Vector | Decision tree | Prediction |
|---|---|---|---|---|
| MAKVIGIDLGTTNSCV…DDNTKKSA | ───────➤ | [0.33, 0.0, 0.0, 0.11, 0.11, 0.22, 0.23, 0.11, 0.22, 0.44, 0.0, 0.0, 0.0, 0.22, 0.0, 0.0, 0.11, 0.0, 0.0, 0.67, 0.0, 0.0, 0.0] | ────────➤ | PF00012 |

B9JZ87_sequence = 'MAKVIGIDLGTTNSCVSVMDGKDAKVIENSEGARTTPSMVAFS' + \
'DDGERLVGQPAKRQAVTNPTNTLFAVKRLIGRRYEDPTVEKDKGLVPFPIIKGDNGDAWVE' + \
'AQGKGYSPAQISAMILQKMKETAEAYLGEKVEKAVITVPAYFNDAQRQATKDAGRIAGLEV' + \
'LRIINEPTAAALAYGLDKTEGKTIAVYDLGGGTFDISVLEIGDGVFEVKSTNGDTFLGGED' + \
'FDMRLVEYLAAEFKKEQGIELKNDKLALQRLKEAAEKAKIELSSSQQTEINLPFITADASG' + \
'PKHLTMKLTRAKFENLVDDLVQRTVAPCKAALKDAGVTAADIDEVVLVGGMSRMPKVQEVV' + \
'KQLFGKEPHKGVNPDEVVAMGAAIQAGVLQGDVKDVLLLDVTPLSLGIETLGGVFTRLIDR' + \
'NTTIPTKKSQVFSTADDNQQAVTIRVSQGEREMAQDNKLLGQFDLVGLPPSPRGVPQIEVT' + \
'FDIDANGIVQVSAKDKGTGKEQQIRIQASGGLSDADIEKMVKDAEANAEADKNRRAVVEAK' + \
'NQAESLIHSTEKSVKDYGDKVSADDRKAIEDAIAALKSSIETSEPNAEDIQAKTQTLMEVS' + \
'MKLGQAIYESQQAEGGAEGGPSGHHDDGIVDADYEEVKDDNTKKSA'
vect = vectorizer.transform([B9JZ87_sequence])
np_vect = np.asarray(vect.todense())[0]
tree_train_vec = vect_dict['uni']['train']
tree = DecisionTreeClassifier(max_depth=4)
tree.fit(tree_train_vec['X'], tree_train_vec['y'])
viz_model = dtreeviz.model(tree, X_train=tree_train_vec['X'], y_train=tree_train_vec['y'],
feature_names=vectorizer.get_feature_names_out(),
class_names=pfam_cat.categories.tolist())
viz_model.view(scale=2, orientation='TD', x=np_vect, fancy=True, show_just_path=True, instance_orientation='LR')
viz_model.view(scale=1.6, orientation='LR', x=np_vect, fancy=False, leaftype='barh', instance_orientation='TD')
Model evaluation
uni_val_vec = vect_dict['uni']['val']
y_true = uni_val_vec['y']
y_hat = best_tree.predict(uni_val_vec['X']).astype(np.int8)
y_hat_proba = best_tree.predict_proba(uni_val_vec['X'])
Confusion matrix
disp = ConfusionMatrixDisplay.from_estimator(
best_tree, uni_val_vec['X'], uni_val_vec['y'], cmap=plt.cm.Greens,
display_labels=pfam_cat.categories, normalize='true'
)
disp.figure_.set_size_inches((12, 12))
ax = disp.ax_
ax.set_title('Confusion matrix (best decision tree)', size=20)
ax.set_xlabel('Predicted family', size=16)
ax.set_ylabel('True family', size=16)
ax.tick_params(axis='both', which='major', labelsize=12)
ax.grid(False)
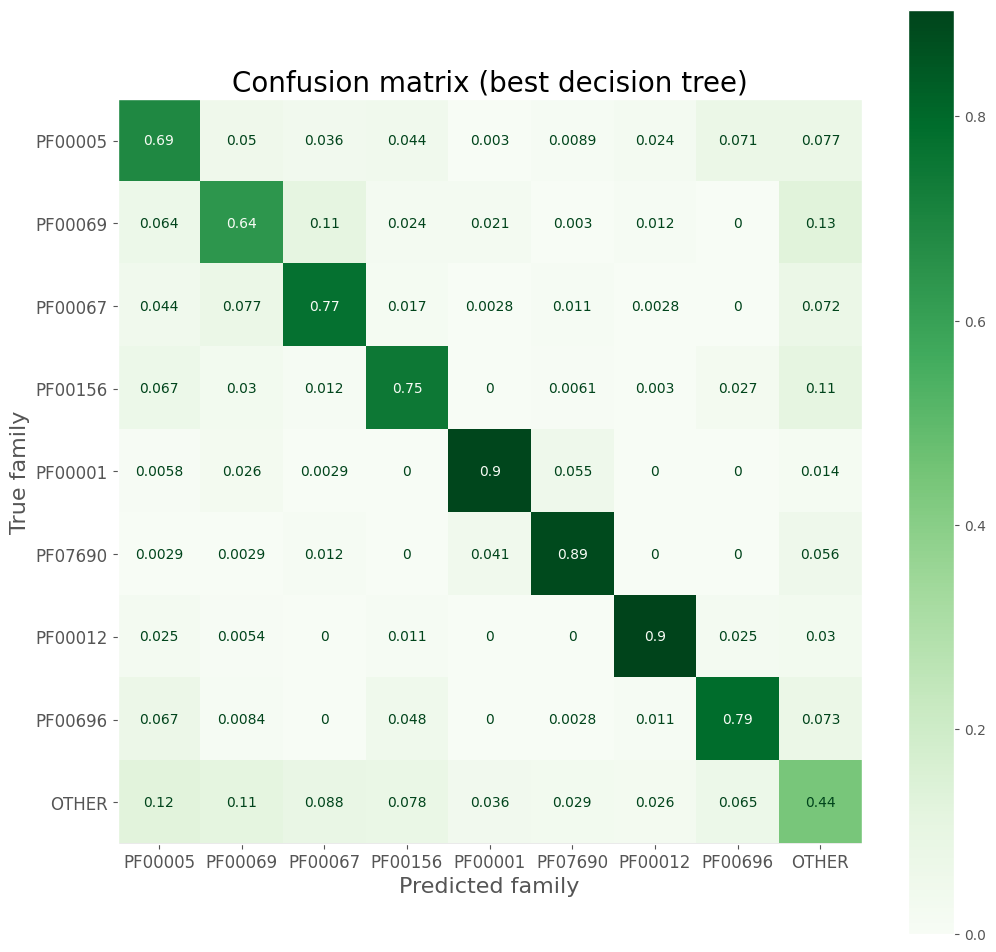
Precision, recall, F1 score
report = classification_report(y_true, y_hat, target_names=pfam_cat.categories, output_dict=True)
pd.DataFrame(report).T.round(2).iloc[:-3]
| precision | recall | f1-score | support | |
|---|---|---|---|---|
| PF00005 | 0.64 | 0.69 | 0.66 | 338.0 |
| PF00069 | 0.67 | 0.64 | 0.65 | 330.0 |
| PF00067 | 0.77 | 0.77 | 0.77 | 362.0 |
| PF00156 | 0.77 | 0.75 | 0.76 | 329.0 |
| PF00001 | 0.90 | 0.90 | 0.90 | 346.0 |
| PF07690 | 0.89 | 0.89 | 0.89 | 341.0 |
| PF00012 | 0.93 | 0.90 | 0.92 | 367.0 |
| PF00696 | 0.82 | 0.79 | 0.80 | 356.0 |
| OTHER | 0.42 | 0.44 | 0.43 | 306.0 |
Best decision tree model
| criterion | gini |
| max_depth | 25 |
| ngram | uni |
tree_eval = pd.DataFrame([
accuracy_score(y_true, y_hat),
], index=['Accuracy'], columns=['Decision tree'])
tree_eval
| Decision tree | |
|---|---|
| Accuracy | 0.757398 |
Random forest
Hyperparameter tunning
| Hyperparameter | Description |
|---|---|
| n_estimators | Number of trees in the forest |
| max_samples | Number of drawn bootstrap samples |
| criterion | Function to measure the quality of a split |
| max_features | Number of features to consider when splitting |
| max_depth | Maximum depth of the tree |
| ngram | Configuration of n-gram vectorizer |
param_grid = ParameterGrid({
'n_estimators': list(itertools.chain(range(1, 20, 6), range(20, 110, 15))),
'max_samples': [i/10 for i in range(1, 6)],
'max_depth': range(1, 6),
'ngram': ['uni', 'bi'],
'criterion': ['gini'],
'max_features': ['log2'],
})
log_forest = pd.DataFrame(columns=['n_estimators', 'max_samples', 'max_features', 'criterion', 'max_depth', 'ngram', 'train_accuracy', 'val_accuracy'])
estimators_forest = []
for params in param_grid:
train_ngram = vect_dict[params['ngram']]['train']
val_ngram = vect_dict[params['ngram']]['val']
ngram = params['ngram']
del params['ngram']
clf = RandomForestClassifier(n_jobs=-1, **params)
clf.fit(train_ngram['X'], train_ngram['y'])
train_accuracy = accuracy_score(train_ngram['y'], clf.predict(train_ngram['X']))
val_accuracy = accuracy_score(val_ngram['y'], clf.predict(val_ngram['X']))
log_forest.loc[len(log_forest.index)] = [params['n_estimators'], params['max_samples'], params['max_features'], params['criterion'], params['max_depth'],
ngram, train_accuracy, val_accuracy]
estimators_forest.append(clf)
top_forests = log_forest.sort_values('val_accuracy', ascending=False)
best_forest = estimators_forest[top_forests.index[0]]
h = top_forests.head(10)
h.index = np.arange(1, len(h)+1)
h
| n_estimators | max_samples | max_features | criterion | max_depth | ngram | train_accuracy | val_accuracy | |
|---|---|---|---|---|---|---|---|---|
| 1 | 80 | 0.4 | log2 | gini | 5 | bi | 0.915477 | 0.909268 |
| 2 | 95 | 0.5 | log2 | gini | 5 | bi | 0.913099 | 0.907642 |
| 3 | 95 | 0.4 | log2 | gini | 5 | bi | 0.915843 | 0.906016 |
| 4 | 95 | 0.2 | log2 | gini | 5 | bi | 0.916392 | 0.902439 |
| 5 | 65 | 0.4 | log2 | gini | 5 | bi | 0.906147 | 0.900813 |
| 6 | 65 | 0.5 | log2 | gini | 5 | bi | 0.907062 | 0.899187 |
| 7 | 80 | 0.3 | log2 | gini | 5 | bi | 0.914014 | 0.897886 |
| 8 | 80 | 0.2 | log2 | gini | 5 | bi | 0.912367 | 0.897236 |
| 9 | 95 | 0.3 | log2 | gini | 5 | bi | 0.915112 | 0.896911 |
| 10 | 80 | 0.5 | log2 | gini | 5 | bi | 0.914929 | 0.896585 |
log_forest.sort_index(inplace=True)
fig, axes = plt.subplots(1, 2, figsize=(12, 6), layout='constrained', sharey=True)
fig.suptitle('Random forest learning curve', size=20)
fig.supxlabel('Number of estimators', size=16)
fig.supylabel('Accuracy', size=16)
df = log_forest[(log_forest['max_samples'] == 0.4) &
(log_forest['max_depth'] == 5) &
(log_forest['ngram'] == 'bi')]
ax = axes[0]
ax.set_title('bigram', size=16)
ax.plot(df['n_estimators'], df['train_accuracy'], label='train', color='black', linewidth=3, alpha=0.5)
ax.plot(df['n_estimators'], df['val_accuracy'], label='validation', color=forest_color, linewidth=3)
ax.axhline(df['val_accuracy'].max(), color='black', linestyle='--', linewidth=1, alpha=0.4)
ax.axhline(df['val_accuracy'].min(), color='black', linestyle='--', linewidth=1, alpha=0.4)
bounderies = [df['val_accuracy'].min().round(3), df['val_accuracy'].max().round(3)]
ticks = [i/100 for i in range(50, 101, 5)]
for b in bounderies:
for tick in ticks:
if abs(tick - b) < 0.02:
ticks.remove(tick)
ax.set_yticks(bounderies + ticks)
for i, tick in enumerate(ax.yaxis.get_major_ticks()):
if i in [0, 1]:
tick.label1.set_size(14)
tick.label1.set_weight(1000)
df = log_forest[(log_forest['max_samples'] == 0.4) &
(log_forest['max_depth'] == 5) &
(log_forest['ngram'] == 'uni')]
ax = axes[1]
ax.set_title('unigram', size=16)
ax.plot(df['n_estimators'], df['train_accuracy'], label='train', color='black', linewidth=3, alpha=0.5)
ax.plot(df['n_estimators'], df['val_accuracy'], label='validation', color=forest_color, linewidth=3)
ax.axhline(df['val_accuracy'].max(), color='black', linestyle='--', linewidth=1, alpha=0.4)
ax.axhline(df['val_accuracy'].min(), color='black', linestyle='--', linewidth=1, alpha=0.4)
ax.legend(loc='upper right')
plt.show()
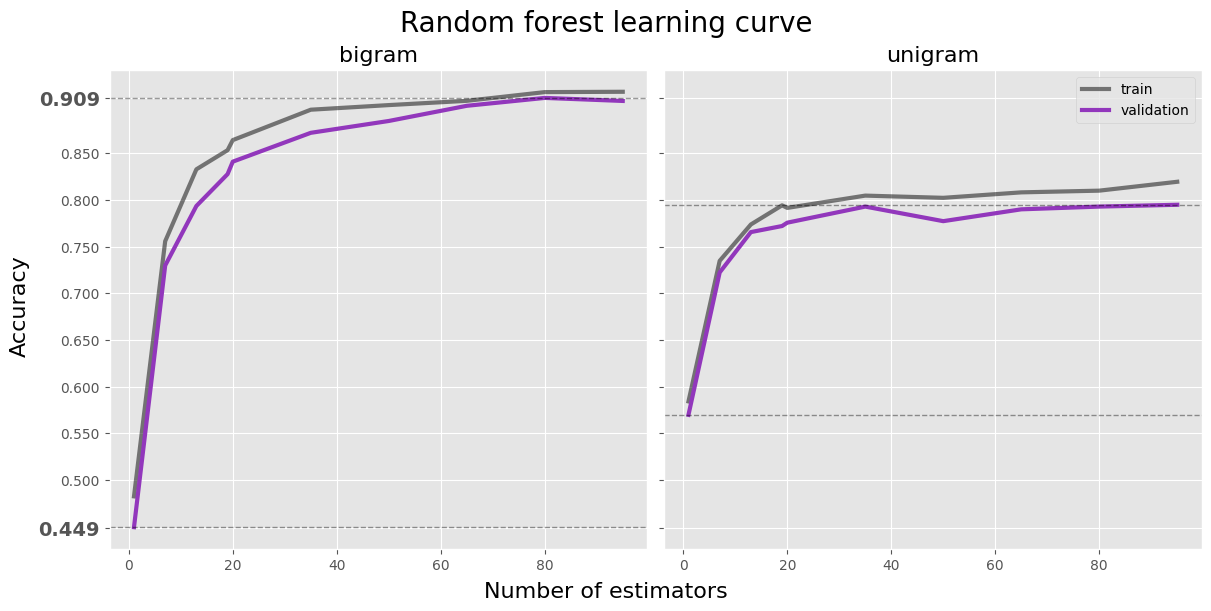
import plotly.express as px
import plotly.io as pio
pio.renderers.default = 'iframe'
df = log_forest.copy()
fig = px.parallel_coordinates(df, color='val_accuracy', range_color=[0, 1],
title='Hyperparameter Parallel Coordinates',
color_continuous_scale=px.colors.sequential.Inferno,
dimensions=['max_depth', 'max_samples', 'n_estimators','val_accuracy'],
template='ggplot2')
fig.show()
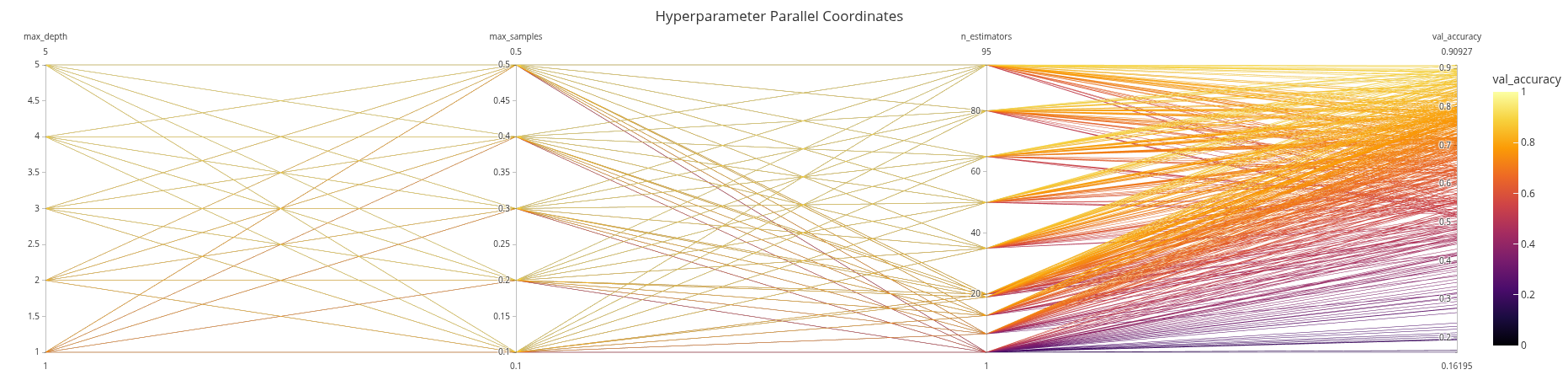
Model evaluation
y_true = bi_val_vec['y']
y_hat = best_forest.predict(bi_val_vec['X']).astype(np.int8)
y_hat_proba = best_forest.predict_proba(bi_val_vec['X'])
Confusion matrix
disp = ConfusionMatrixDisplay.from_estimator(
best_forest, bi_val_vec['X'], bi_val_vec['y'], cmap=plt.cm.Purples,
display_labels=pfam_cat.categories, normalize='true'
)
disp.figure_.set_size_inches((12, 12))
ax = disp.ax_
ax.set_title('Confusion matrix (best random forest)', size=20)
ax.set_xlabel('Predicted family', size=16)
ax.set_ylabel('True family', size=16)
ax.tick_params(axis='both', which='major', labelsize=12)
ax.grid(False)
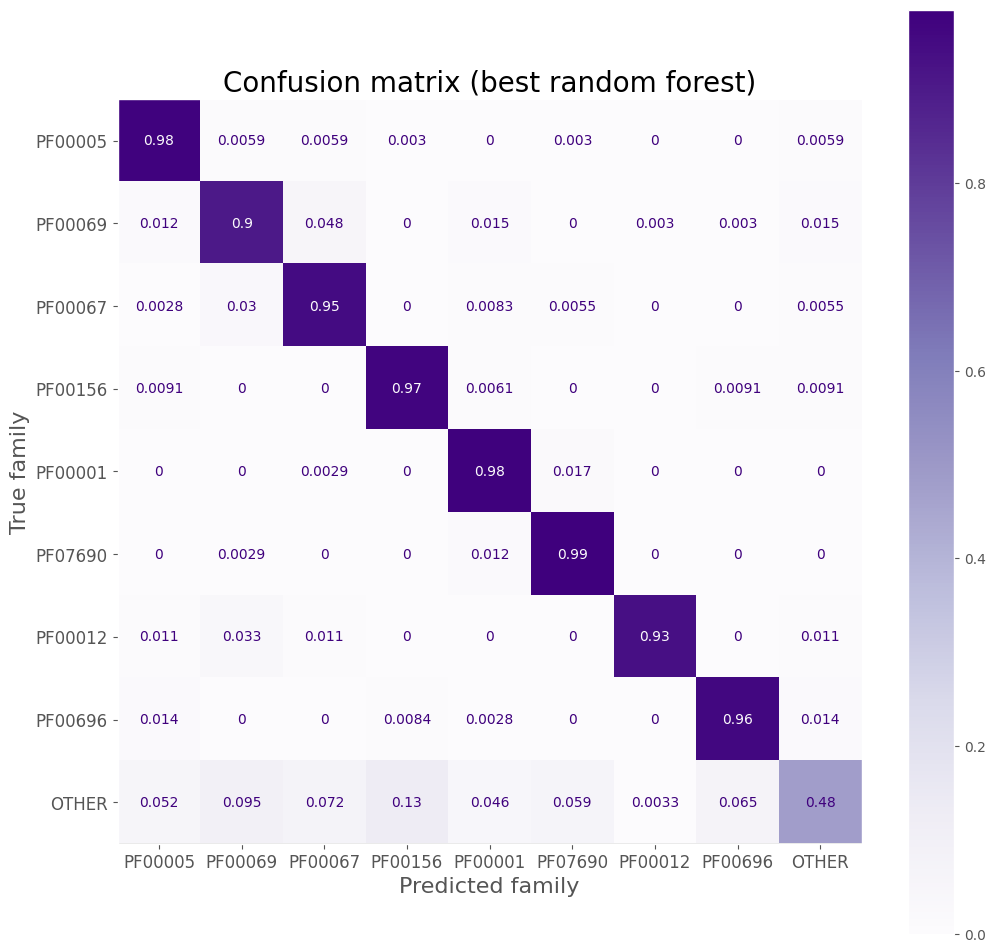
Precision, recall, F1 score
report = classification_report(y_true, y_hat, target_names=pfam_cat.categories, output_dict=True)
pd.DataFrame(report).T.round(2).iloc[:-3]
| precision | recall | f1-score | support | |
|---|---|---|---|---|
| PF00005 | 0.91 | 0.98 | 0.94 | 338.0 |
| PF00069 | 0.84 | 0.90 | 0.87 | 330.0 |
| PF00067 | 0.88 | 0.95 | 0.91 | 362.0 |
| PF00156 | 0.88 | 0.97 | 0.92 | 329.0 |
| PF00001 | 0.92 | 0.98 | 0.95 | 346.0 |
| PF07690 | 0.93 | 0.99 | 0.95 | 341.0 |
| PF00012 | 0.99 | 0.93 | 0.96 | 367.0 |
| PF00696 | 0.93 | 0.96 | 0.95 | 356.0 |
| OTHER | 0.88 | 0.48 | 0.62 | 306.0 |
Best random forest model
| n_estimators | 80 |
| max_samples | 0.4 |
| max_features | log2 |
| criterion | gini |
| max_depth | 5 |
| ngram | bi |
forest_eval = pd.DataFrame([
accuracy_score(y_true, y_hat),
], index=['Accuracy'], columns=['Random forest'])
forest_eval
| Random forest | |
|---|---|
| Accuracy | 0.909268 |
Final model
Comparing models
eval = pd.concat([forest_eval.T, knn_eval.T, tree_eval.T]).round(3)
eval
| Accuracy | |
|---|---|
| Random forest | 0.909 |
| KNN | 0.873 |
| Decision tree | 0.757 |
fig, ax = plt.subplots(1, 1, figsize=(12, 5))
ax.set_title('Accuracy')
bars = ax.bar(eval.index, eval.loc[:, 'Accuracy'], color=[forest_color, knn_color, tree_color], width=0.5)
ax.set_ylim(0, 1)
ax.bar_label(bars)
plt.show()
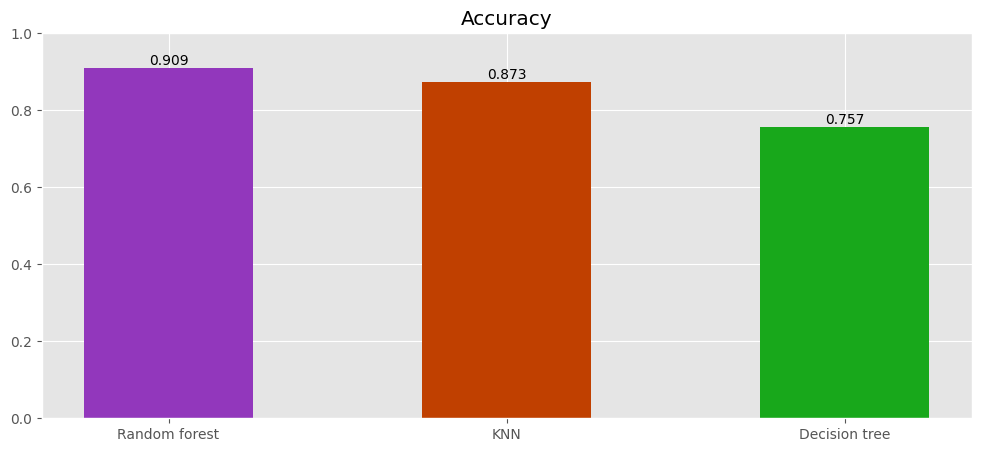
Random forest achieves the highest accuracy.
best_model = best_forest
Evaluation on the test set
To evaluate the model on the imbalanced test set, we use the weighted \(F_1\) score.
\[ \text{F}_{1, \text{weighted}}(y, \hat{y}) = \sum_{k} \frac{|\{y_i \in y \mid y_i = k\}|}{|\{y_i \in y\}|} \left( 2 \frac{P \cdot R}{P + R} \right) \]bi_test_vec = vect_dict['bi']['test']
y_true = bi_test_vec['y']
y_hat = best_model.predict(bi_test_vec['X']).astype(np.int8)
y_hat_proba = best_model.predict_proba(bi_test_vec['X'])
pd.DataFrame([accuracy_score(y_true, y_hat),
f1_score(y_true, y_hat, average='weighted')],
index=['Test accuracy', 'Weighted F1 score'],
columns=[''])
| Test accuracy | 0.880642 |
|---|---|
| Weighted F1 score | 0.870774 |
Confusion matrix
disp = ConfusionMatrixDisplay.from_estimator(
best_model, bi_test_vec['X'], y_true, cmap=plt.cm.Blues,
display_labels=pfam_cat.categories, normalize='true'
)
disp.figure_.set_size_inches((12, 12))
ax = disp.ax_
ax.set_title('Confusion matrix (best model, test data)', size=20)
ax.set_xlabel('Predicted family', size=16)
ax.set_ylabel('True family', size=16)
ax.tick_params(axis='both', which='major', labelsize=12)
ax.grid(False)
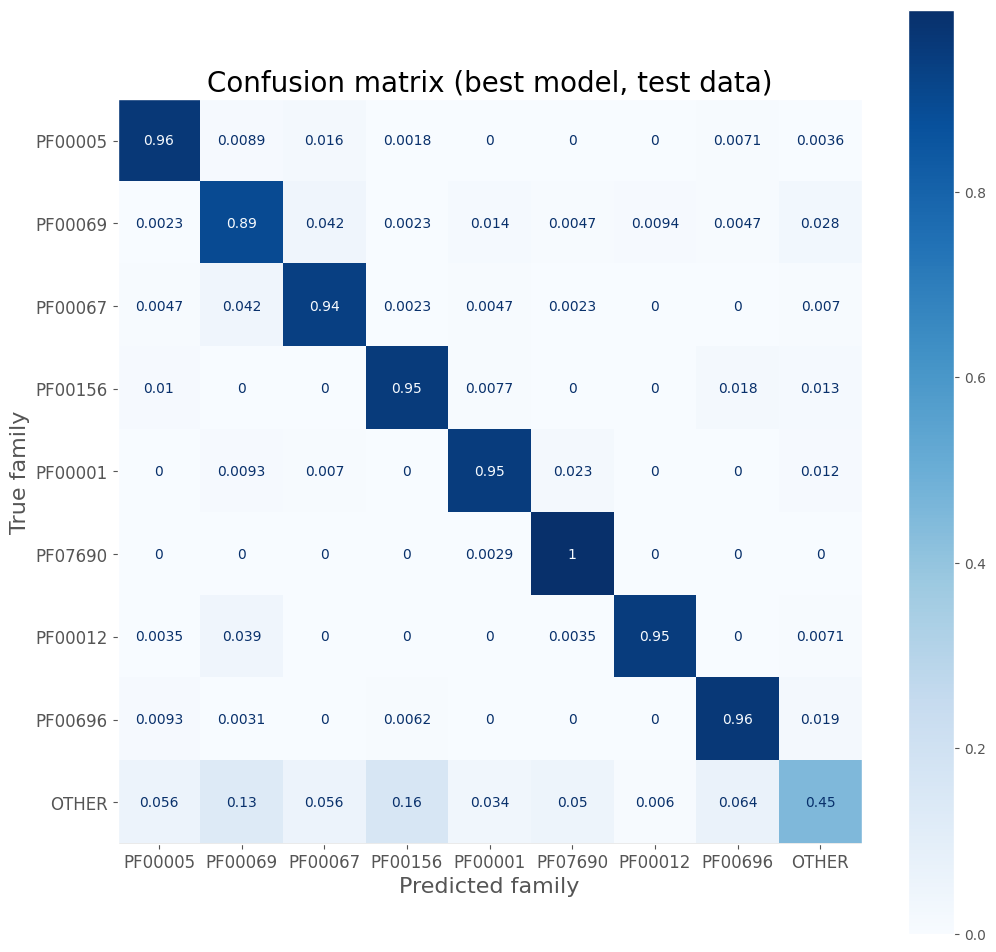
The model is weakest when classifying the “other” class, which is often confused with one of the priority families.
Precision a recall, F1 score
| Precision \(P\) | Recall \(R\) | \(F_1\) score |
|---|---|---|
| \[ \frac{T_p}{T_p + F_p} \] | \[ \frac{T_p}{T_p + F_n} \] | \[ 2 \frac{P \cdot R}{P + R} \] |
report = classification_report(y_true, y_hat, target_names=pfam_cat.categories, output_dict=True)
pd.DataFrame(report).T.round(2).iloc[:-3]
| precision | recall | f1-score | support | |
|---|---|---|---|---|
| PF00005 | 0.93 | 0.96 | 0.95 | 562.0 |
| PF00069 | 0.79 | 0.89 | 0.84 | 426.0 |
| PF00067 | 0.87 | 0.94 | 0.90 | 427.0 |
| PF00156 | 0.81 | 0.95 | 0.88 | 390.0 |
| PF00001 | 0.93 | 0.95 | 0.94 | 430.0 |
| PF07690 | 0.90 | 1.00 | 0.94 | 339.0 |
| PF00012 | 0.97 | 0.95 | 0.96 | 282.0 |
| PF00696 | 0.87 | 0.96 | 0.92 | 322.0 |
| OTHER | 0.86 | 0.45 | 0.59 | 500.0 |
fig, axes = plt.subplots(3, 3, figsize=(12, 10), layout='constrained')
fig.suptitle('Precision recall curve', fontsize=20)
fig.supxlabel('Recall', size=16)
fig.supylabel('Precision', size=16)
for i, (cat, ax) in enumerate(zip(pfam_cat.categories, fig.axes)):
disp = PrecisionRecallDisplay.from_predictions(y_true == i, y_hat_proba[:, i], ax=ax, name=cat, linewidth=1.5, alpha=1, color=main_color)
ax.set(xlabel=None, ylabel=None)
plt.show()
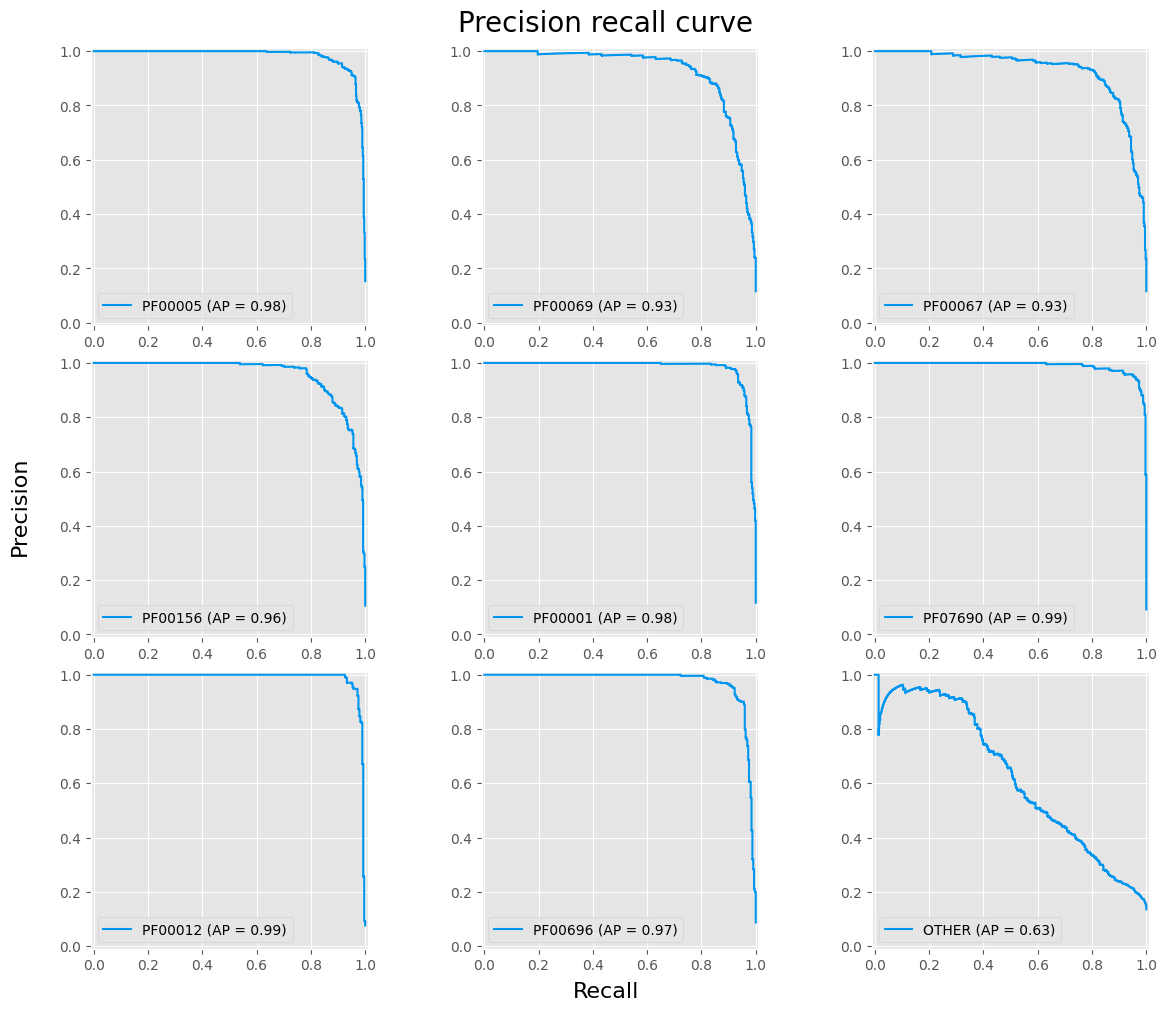
ROC a AUC
The ROC curve is a plot of the ratio of FPR and TPR versus the parameterized threshold.
$$ \text{TPR} = \frac{\text{TP}}{\text{TP + FN}} \qquad \text{FPR} = \frac{\text{FP}}{\text{FP + TN}} $$
fig, axes = plt.subplots(3, 3, figsize=(12, 10), layout='constrained')
fig.suptitle('ROC curve', fontsize=20)
fig.supxlabel('False positive rate', size=16)
fig.supylabel('True postive rate', size=16)
for i, (cat, ax) in enumerate(zip(pfam_cat.categories, fig.axes)):
disp = RocCurveDisplay.from_predictions(y_true == i, y_hat_proba[:, i], ax=ax, name=f'{cat} vs the rest', linewidth=1.5, color=main_color)
ax.plot([(0, 0), (1, 1)], color='k', alpha=0.5, linestyle='--', linewidth=0.8)
ax.set(xlabel=None, ylabel=None)
plt.show()
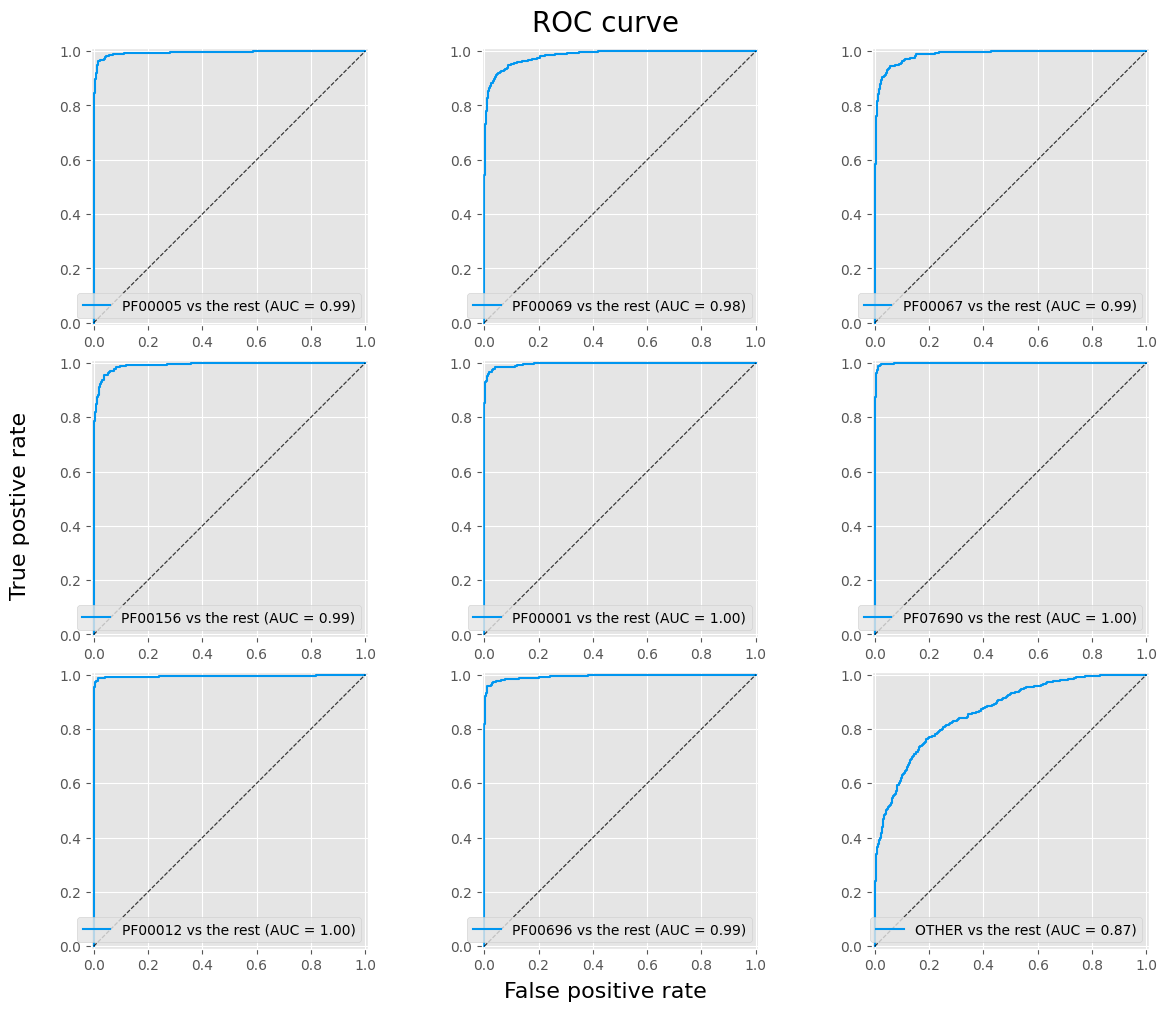
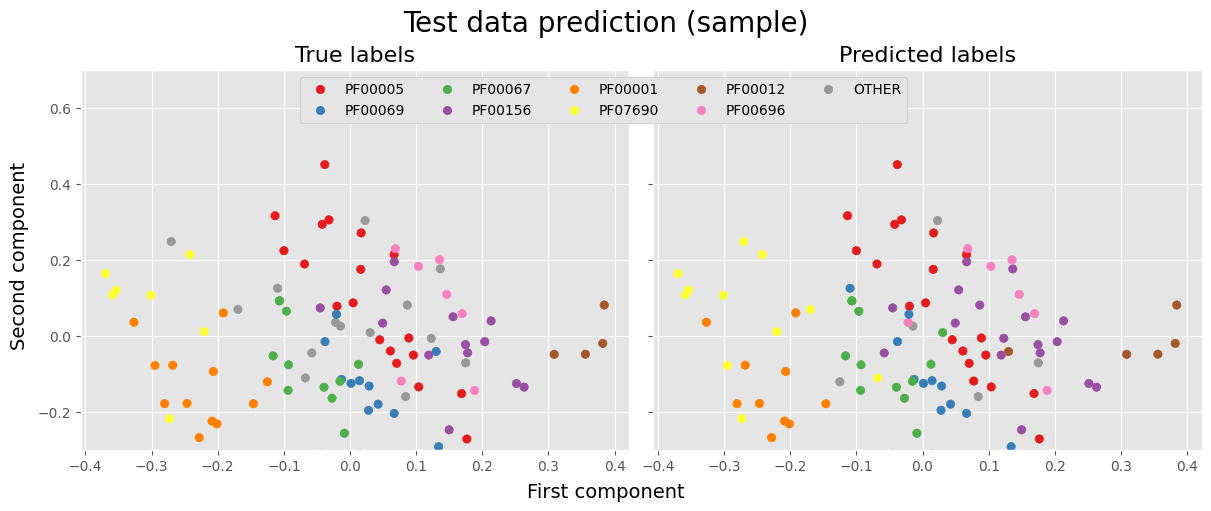
Visualization of the classification on sample data
In the following example, we visualize the success of the model on a sample of 100 test data. We represent the values by projecting them onto the first two PCA components.
pca = PCA(n_components=2)
pca_X = pca.fit_transform(bi_test_vec['X'])
fig, axes = plt.subplots(1, 2, figsize=(12, 5), layout='constrained', sharey=True)
fig.suptitle('Test data prediction (sample)', size=20)
fig.supxlabel('First component', size=14)
fig.supylabel('Second component', size=14)
rs = np.random.RandomState(2)
sample = rs.choice(np.arange(len(y_true)), 100, replace=False)
ax = axes[0]
ax.scatter(pca_X[sample, 0], pca_X[sample, 1], c=(y_true[sample]), cmap='Set1')
ax.set_title('True labels', size=16)
ax = axes[1]
scatter = ax.scatter(pca_X[sample, 0], pca_X[sample, 1], c=(y_hat[sample]), cmap='Set1')
ax.set_title('Predicted labels', size=16)
legend1 = ax.legend(scatter.legend_elements()[0], pfam_cat.categories.tolist(), ncol=5, loc='upper center',
fancybox=True, framealpha=1, bbox_to_anchor=(-0.09, 1), fontsize=10)
ax.add_artist(legend1)
ax.set_ylim(-0.3, 0.7)
plt.show()
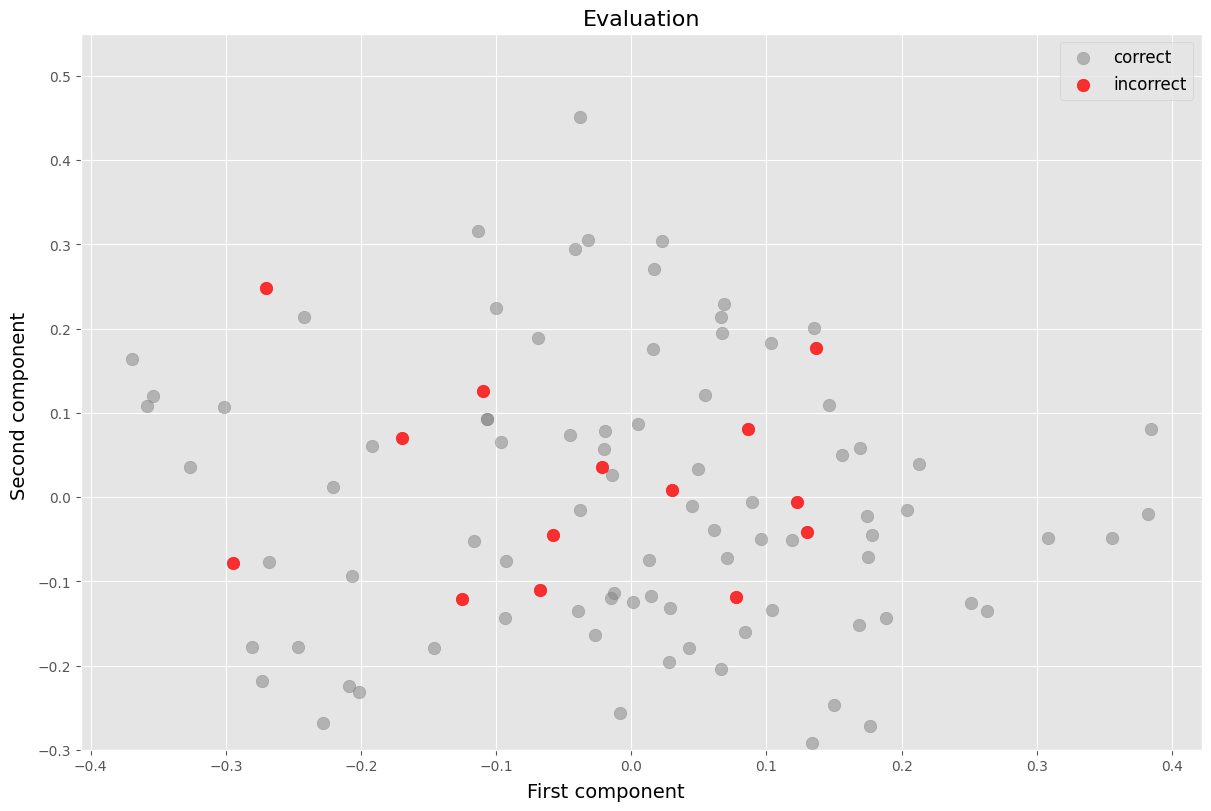
pca = PCA(n_components=2)
pca_X = pca.fit_transform(bi_test_vec['X'])
fig, ax = plt.subplots(1, 1, figsize=(12, 8), layout='constrained', sharey=True)
fig.supxlabel('First component', size=14)
fig.supylabel('Second component', size=14)
correct = sample[y_true[sample] == y_hat[sample]]
inccorect = sample[y_true[sample] != y_hat[sample]]
ax.scatter(pca_X[correct, 0], pca_X[correct, 1], c='grey', alpha=0.5, label='correct', s=80)
ax.scatter(pca_X[inccorect, 0], pca_X[inccorect, 1], c='red', alpha=0.8, label='incorrect', s=80)
ax.set_title('Evaluation', size=16)
ax.legend(loc='upper right', fontsize=12)
ax.set_ylim(-0.3, 0.55)
plt.show()