Data is sourced from the Prague Public Transport Open Data portal, specifically the GTFS (General Transit Feed Specification) timetables.
import collections
import math
import warnings
import contextily as ctx
import matplotlib as mpl
import matplotlib.cm as cm
import matplotlib.colors as mcolors
import matplotlib.font_manager as fm
import matplotlib.patches as mpatches
import matplotlib.pyplot as plt
import networkx as nx
import numpy as np
import pandas as pd
import pywaffle as waff
from mpl_toolkits.axes_grid1.anchored_artists import AnchoredSizeBar
from matplotlib.lines import Line2D
warnings.simplefilter(action="ignore", category=UserWarning)
warnings.simplefilter(action="ignore", category=DeprecationWarning)
np.random.seed(1)
plt.style.use("ggplot")
font = fm.FontProperties(size=9)
red = (226 / 255, 74 / 255, 51 / 255)
redl = (226 / 255, 74 / 255, 51 / 255, 0.6)
redf = (226 / 255, 74 / 255, 51 / 255, 1)
blue = (52 / 255, 138 / 255, 189 / 255)
grey = (100 / 255, 100 / 255, 100 / 255)
📚 Dataset
The datasets are loaded into memory, and basic information for preprocessing is displayed.
conns = pd.read_csv("d.csv")
stops = pd.read_csv("stops.txt")
conns.head()
| stop_from | stop_from_name | stop_to | stop_to_name | depart_from | arrive_to | route_type | is_night | monday | tuesday | wednesday | thursday | friday | saturday | sunday | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | U2991Z301 | Hněvice | T58005 | Hněvice seř.n. | 4:53:00 | 4:54:30 | 2 | 0 | 1 | 1 | 1 | 1 | 1 | 0 | 0 |
| 1 | T58005 | Hněvice seř.n. | U4610Z301 | Záluží | 4:54:30 | 4:56:00 | 2 | 0 | 1 | 1 | 1 | 1 | 1 | 0 | 0 |
| 2 | U4610Z301 | Záluží | U4609Z301 | Dobříň | 4:56:00 | 4:59:00 | 2 | 0 | 1 | 1 | 1 | 1 | 1 | 0 | 0 |
| 3 | U4609Z301 | Dobříň | U4608Z301 | Roudnice nad Labem | 4:59:00 | 5:03:00 | 2 | 0 | 1 | 1 | 1 | 1 | 1 | 0 | 0 |
| 4 | U4608Z301 | Roudnice nad Labem | U4609Z301 | Dobříň | 4:36:00 | 4:38:00 | 2 | 0 | 1 | 1 | 1 | 1 | 1 | 0 | 0 |
conns.info()
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 1642433 entries, 0 to 1642432
Data columns (total 15 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 stop_from 1642433 non-null object
1 stop_from_name 1642433 non-null object
2 stop_to 1642433 non-null object
3 stop_to_name 1642433 non-null object
4 depart_from 1642433 non-null object
5 arrive_to 1642433 non-null object
6 route_type 1642433 non-null int64
7 is_night 1642433 non-null int64
8 monday 1642433 non-null int64
9 tuesday 1642433 non-null int64
10 wednesday 1642433 non-null int64
11 thursday 1642433 non-null int64
12 friday 1642433 non-null int64
13 saturday 1642433 non-null int64
14 sunday 1642433 non-null int64
dtypes: int64(9), object(6)
memory usage: 188.0+ MB
stops.head()
| stop_id | stop_name | stop_lat | stop_lon | zone_id | stop_url | location_type | parent_station | wheelchair_boarding | level_id | platform_code | asw_node_id | asw_stop_id | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | U50S1 | Budějovická | 50.044411 | 14.448787 | P | NaN | 1 | NaN | 1 | NaN | NaN | 50.0 | NaN |
| 1 | U52S1 | Chodov | 50.031672 | 14.490961 | P | NaN | 1 | NaN | 1 | NaN | NaN | 52.0 | NaN |
| 2 | U75S1 | Kolbenova | 50.110395 | 14.516398 | P | NaN | 1 | NaN | 1 | NaN | NaN | 75.0 | NaN |
| 3 | U78S1 | Ládví | 50.126591 | 14.469451 | P | NaN | 1 | NaN | 1 | NaN | NaN | 78.0 | NaN |
| 4 | U100S1 | Vltavská | 50.100298 | 14.438492 | P | NaN | 1 | NaN | 1 | NaN | NaN | 100.0 | NaN |
stops.info()
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 16435 entries, 0 to 16434
Data columns (total 13 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 stop_id 16435 non-null object
1 stop_name 15936 non-null object
2 stop_lat 16435 non-null float64
3 stop_lon 16435 non-null float64
4 zone_id 15408 non-null object
5 stop_url 0 non-null float64
6 location_type 16435 non-null int64
7 parent_station 954 non-null object
8 wheelchair_boarding 16435 non-null int64
9 level_id 954 non-null object
10 platform_code 14750 non-null object
11 asw_node_id 15748 non-null float64
12 asw_stop_id 15354 non-null float64
dtypes: float64(5), int64(2), object(6)
memory usage: 1.6+ MB
⚙️ Data Preprocessing
This section details the transformation of key features into the correct formats and discards unused values.
The output of this section is two clean datasets: conns (connections) and stops (stops).
🚈 Connections - conns
⏳ Time Data
Time columns are converted to the correct format and validated. Each time value is represented by three columns: H, M, S.
def split_time_column(df, col):
colH, colM, colS = f"{col}_H", f"{col}_M", f"{col}_S"
cols = [colH, colM, colS]
slice = df.loc[:, col].str.split(":", expand=True).astype("int64")
slice[cols] = slice
slice[colH] = slice[colH].mod(24)
return slice[cols], cols
for col in ["depart_from", "arrive_to"]:
if col in conns.columns:
slice, cols = split_time_column(conns, col)
conns.drop(col, axis=1, inplace=True)
conns[cols] = slice
def to_timedelta(df, h_col, m_col, s_col):
seconds = 3600 * df[h_col] + 60 * df[m_col] + df[s_col]
return seconds
departures = to_timedelta(conns, "depart_from_H", "depart_from_M", "depart_from_S")
arrivals = to_timedelta(conns, "arrive_to_H", "arrive_to_M", "arrive_to_S")
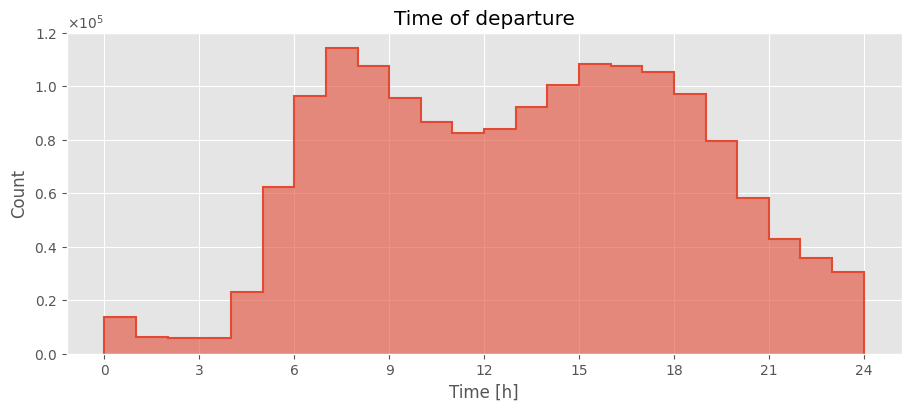
fig, ax = plt.subplots(1, 1, figsize=(9, 4), layout="constrained")
ax.set_title("Time of departure")
ax.hist(departures / 3600, bins=24, range=(0, 24), alpha=0.6)
ax.hist(departures / 3600, bins=24, range=(0, 24), histtype="step", color=red, linewidth=1.5)
ax.set_xlabel("Time [h]")
ax.set_ylabel("Count")
ax.ticklabel_format(axis="y", style="sci", scilimits=(0, 0), useMathText=True)
ax.set_xticks(range(0, 25, 3));
📅 Days of the Week and Service Type
Relevant values are converted to a categorical type.
days = ["monday", "tuesday", "wednesday", "thursday", "friday", "saturday", "sunday"]
for col in ["is_night", *days]:
conns[col] = conns[col].astype("boolean")
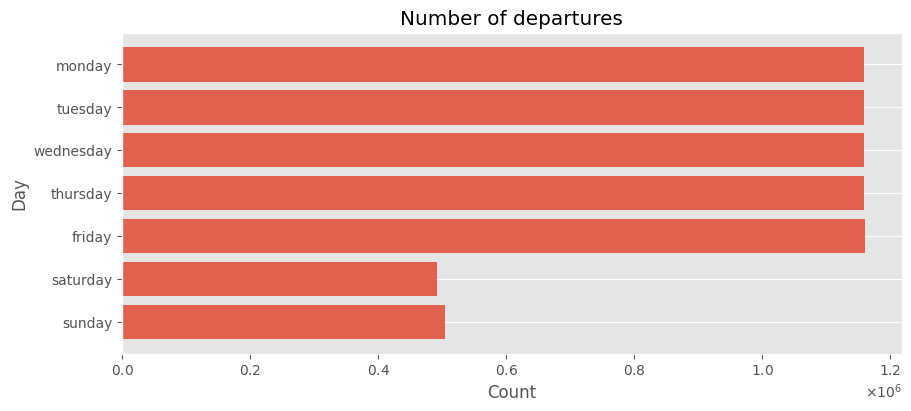
days_dist = pd.DataFrame(conns[days].sum(), columns=["count"])
days_dist.style.format(precision=3, thousands=" ", decimal=".").format_index(str.upper, axis=0).format_index(str.upper, axis=1)
| COUNT | |
|---|---|
| MONDAY | 1 159 992 |
| TUESDAY | 1 159 986 |
| WEDNESDAY | 1 159 986 |
| THURSDAY | 1 159 986 |
| FRIDAY | 1 160 097 |
| SATURDAY | 492 743 |
| SUNDAY | 504 771 |
fig, ax = plt.subplots(1, 1, figsize=(9, 4), layout="constrained")
ax.set_title("Number of departures")
ax.barh(days_dist["count"].index, days_dist["count"], alpha=0.85)
ax.set_ylabel("Day")
ax.set_xlabel("Count")
ax.ticklabel_format(axis="x", style="sci", scilimits=(0, 0), useMathText=True)
ax.invert_yaxis()
ax.grid(visible=False, which="major", axis="x")
🪪 Stop IDs
Unused stop IDs are dropped. Stops are identified by name.
conns.drop(["stop_from", "stop_to"], axis=1, inplace=True, errors="ignore")
🚢 Transport Modes
Transport modes are converted to a categorical data type.
route_type_map = {
0: "Tram",
1: "Metro",
2: "Rail",
3: "Bus",
4: "Ferry",
7: "Funicular",
}
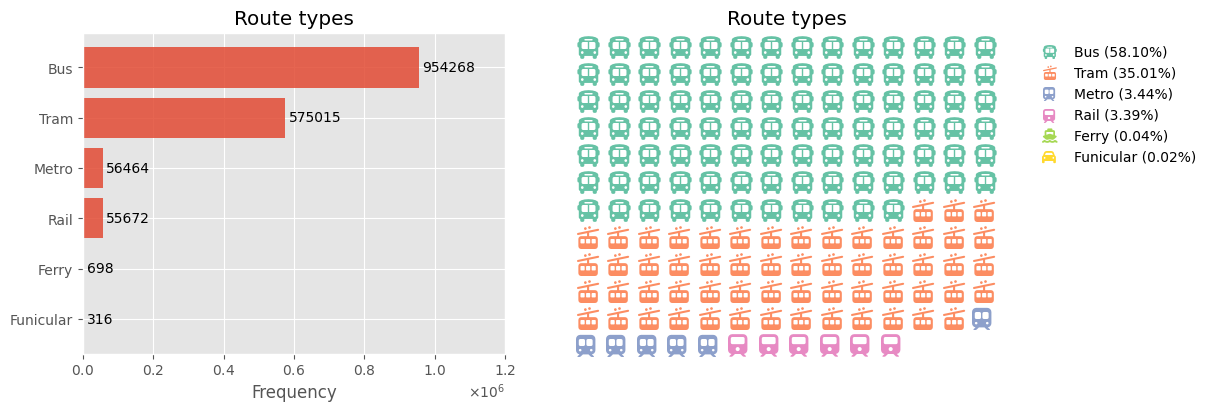
conns["route_type"] = (conns["route_type"].map(route_type_map, na_action="ignore").astype("category"))
types = conns["route_type"].value_counts()
fig, axes = plt.subplots(1, 2, figsize=(12, 4), layout="constrained", gridspec_kw={"wspace": 0.1})
ax = axes[0]
ax.set_title("Route types")
ax.set_xlabel("Frequency")
ax.ticklabel_format(axis="x", style="sci", scilimits=(0, 0), useMathText=True)
bars = ax.barh(types.index, types, alpha=0.85)
ax.invert_yaxis()
ax.set_xlim(0, 1.2 * 10**6)
for bar, count in zip(bars, types):
ax.text(bar.get_width() + 10**4, bar.get_y() + bar.get_height() / 2, f"{count}", va="center", fontsize=10)
val = types / 10000
val_freq = val / val.sum()
waff.Waffle.make_waffle(
ax=axes[1], rows=12, values=val,
title={"label": "Route types", "loc": "center"},
labels=[f"{k} ({v*100:.2f}%)" for k, v in val_freq.items()],
legend={"bbox_to_anchor": (1.5, 1), "ncol": 1, "framealpha": 0},
icons=["bus", "train-tram", "train-subway", "train", "ship", "car"],
font_size=16, icon_style="solid", icon_legend=True, starting_location="NW",
vertical=True, cmap_name="Set2",
)
🚏 Stops - stops
🧭 Coordinates
Only coordinates are used from the stops dataset for plotting connections. Other features are discarded.
For stops with identical names, their average coordinates are used. Minor name variations for the same physical stops are not addressed here but will be manually adjusted later if needed.
stops = stops[["stop_name", "stop_lat", "stop_lon"]]
stops = stops.groupby(by=["stop_name"], dropna=True).mean()
🏭 Preprocessing Summary
After preprocessing, the two clean datasets, conns and stops, appear as follows (time columns are omitted for brevity):
conns.drop(['depart_from_H', 'depart_from_M', 'depart_from_S', 'arrive_to_H', 'arrive_to_M', 'arrive_to_S'], axis=1).head()
| stop_from_name | stop_to_name | route_type | is_night | monday | tuesday | wednesday | thursday | friday | saturday | sunday | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | Hněvice | Hněvice seř.n. | Rail | False | True | True | True | True | True | False | False |
| 1 | Hněvice seř.n. | Záluží | Rail | False | True | True | True | True | True | False | False |
| 2 | Záluží | Dobříň | Rail | False | True | True | True | True | True | False | False |
| 3 | Dobříň | Roudnice nad Labem | Rail | False | True | True | True | True | True | False | False |
| 4 | Roudnice nad Labem | Dobříň | Rail | False | True | True | True | True | True | False | False |
stops.head()
| stop_lat | stop_lon | |
|---|---|---|
| stop_name | ||
| AHr Km 11,485 | 50.146550 | 14.731470 |
| Albertov | 50.067917 | 14.420798 |
| Ametystová | 49.988201 | 14.362216 |
| Amforová | 50.041778 | 14.327298 |
| Anděl | 50.071132 | 14.403406 |
🕸️ Network Analysis
This section covers:
- Constructing the transport network.
- Visualizing key subgraphs.
- Performing basic node analysis.
🛠️ Graph Construction
stop_pos = {n: np.array([c["stop_lon"], c["stop_lat"]]) for n, c in stops.iterrows()}
nodes = [(n, s.to_dict()) for n, s in stops.iterrows()]
# G.add_nodes_from(nodes)
def extract_edges(df):
cc = df[["stop_from_name", "stop_to_name"]].copy()
cc[["stop_from_name", "stop_to_name"]] = np.sort(cc[["stop_from_name", "stop_to_name"]], axis=1)
cc["count"] = 1
cc = cc.groupby(["stop_from_name", "stop_to_name"]).sum().reset_index()
cc = [(s["stop_from_name"], s["stop_to_name"], s["count"]) for _, s in cc.iterrows()]
return cc
def build_graph(conns):
edges = extract_edges(conns)
g = nx.Graph()
g.add_weighted_edges_from(edges)
return g
G = build_graph(conns)
G.remove_node("Praha Masarykovo nádr.")
G.remove_node("Pha hl.n. Lc201,202")
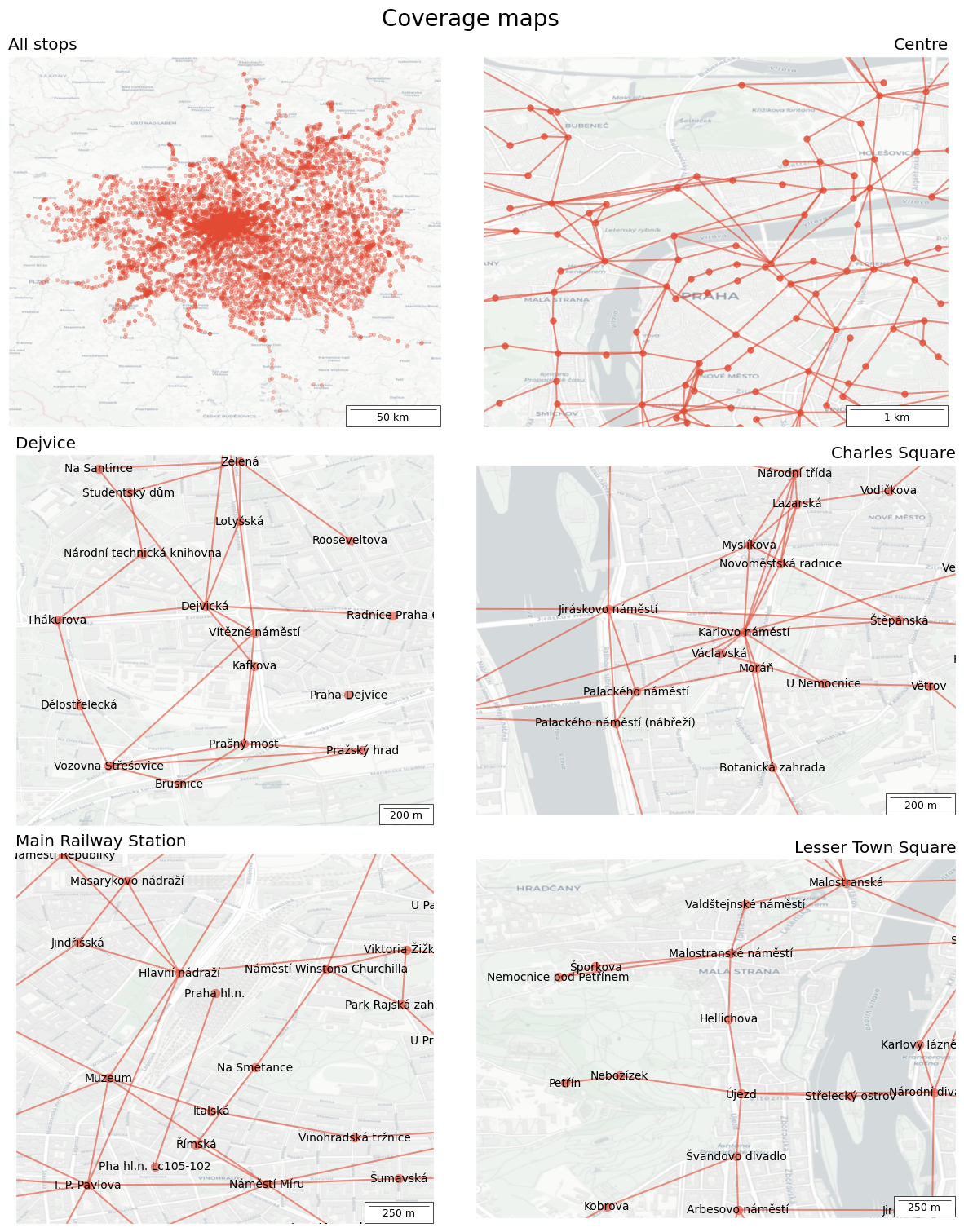
🎨 Graph and Subgraph Visualization
- The overall coverage of Prague (and surrounding areas).
- Prague city center.
- Dejvice.
- Charles Square.
- Main Railway Station.
- Lesser Town.
def subgroup_map_filter(g, m, lat="stop_lat", lon="stop_lon"):
def filter_subgroup(lbc, urc):
filtered = m[(lbc[0] < m[lat]) & (m[lat] < urc[0]) & (lbc[1] < m[lon]) & (m[lon] < urc[1])]
return g.subgraph(filtered.index)
return filter_subgroup
def subgroup_distance_filter(g, m, lat="stop_lat", lon="stop_lon"):
def filter_subgroup(coor, dist):
x, y = coor
dx = m[lat] - x
dy = m[lon] - y
dists = np.sqrt(dx * dx + dy * dy)
filtered = m[dists < dist]
return g.subgraph(filtered.index)
return filter_subgroup
def subgroup_distance_filter_inv(g, m, lat="stop_lat", lon="stop_lon"):
def filter_subgroup(coor, dist):
x, y = coor
dx = m[lat] - x
dy = m[lon] - y
dists = np.sqrt(dx * dx + dy * dy)
filtered = m[dists > dist]
return g.subgraph(filtered.index)
return filter_subgroup
def add_scalebar(ax, s, loc="lower right", label_top=False):
txt = ""
if s > 0.008:
txt = f"{round(s * 10**2)} km"
else:
txt = f"{round(s * 10**5)} m"
scalebar = AnchoredSizeBar(ax.transData, s, txt, loc, label_top=label_top, fontproperties=font, pad=0.4)
ax.add_artist(scalebar)
filter = subgroup_map_filter(G, stops)
filter_d = subgroup_distance_filter(G, stops)
filter_d_inv = subgroup_distance_filter_inv(G, stops)
def add_map(ax, source, scale, reset_extent=True):
ctx.add_basemap(ax=ax, crs="WGS84", source=ctx.providers.CartoDB.Positron, reset_extent=True, attribution=False)
ax.grid(False)
add_scalebar(ax, scale)
def draw_part(ax, title, title_loc, A, B, radius, node_param, edge_param):
ax.set_title(title, loc=title_loc)
ax.set_xlim(A[1], B[1])
ax.set_ylim(A[0], B[0])
M = (np.array(A) + np.array(B)) / 2
g = filter_d(M, radius)
nx.draw_networkx_nodes(g, pos=stop_pos, ax=ax, node_size=node_param["size"], node_color=node_param["color"], alpha=node_param["alpha"])
nx.draw_networkx_edges(g, pos=stop_pos, ax=ax, width=edge_param["size"], edge_color=edge_param["color"], alpha=edge_param["alpha"])
def draw_part_with_label(ax, title, title_loc, A, B, radius, params):
ax.set_title(title, loc=title_loc)
ax.set_xlim(A[1], B[1])
ax.set_ylim(A[0], B[0])
M = (np.array(A) + np.array(B)) / 2
g = filter_d(M, radius)
nx.draw_networkx(g, pos=stop_pos, ax=ax, node_size=params["node_size"], node_color=params["node_color"], width=params["width"],
font_size=params["font_size"], edge_color=params["edge_color"], with_labels=True)
centre = ["Centre", [50.07347057153624, 14.396852618086926], [50.11329080577483, 14.44677177212586], 0.04]
dejvice = ["Dejvice", [50.09122027369268, 14.385020433301096], [50.10756165438437, 14.403450996019187], 0.01]
charles = ["Charles Square", [50.069188151071394, 14.40950684182552], [50.08070937389346, 14.425281091947769], 0.02]
station = ["Main Railway Station", [50.07344788999524, 14.4278631463291], [50.088977084459446, 14.44535284907064], 0.02]
lesser = ["Lesser Town Square", [50.075600319200056, 14.392449133622146], [50.09242635204253, 14.414991205632134], 0.03]
nparam1 = {"size": 30, "color": red, "alpha": 0.8}
eparam1 = {"size": 1.5, "color": red, "alpha": 0.6}
params1 = {"node_size": 60, "node_color": redl, "width": 1.5, "font_size": 10, "edge_color": redl}
fig, axes = plt.subplots(3, 2, figsize=(12, 15), layout="constrained")
fig.suptitle("Coverage maps", fontsize=20)
ax = axes[0][0]
ax.set_title("All stops", loc="left")
nx.draw_networkx_nodes(G, pos=stop_pos, ax=ax, node_size=10, node_color=red, alpha=0.3)
add_map(ax, ctx.providers.CartoDB.Positron, 0.5)
ax = axes[0][1]
loc = centre
draw_part(ax, loc[0], "right", loc[1], loc[2], loc[3], nparam1, eparam1)
add_map(ax, ctx.providers.CartoDB.Positron, 0.01)
ax = axes[1][0]
loc = dejvice
draw_part_with_label(ax, loc[0], "left", loc[1], loc[2], loc[3], params1)
add_map(ax, ctx.providers.CartoDB.Positron, 0.002)
ax = axes[1][1]
loc = charles
draw_part_with_label(ax, loc[0], "right", loc[1], loc[2], loc[3], params1)
add_map(ax, ctx.providers.CartoDB.Positron, 0.002)
ax = axes[2][0]
loc = station
draw_part_with_label(ax, loc[0], "left", loc[1], loc[2], loc[3], params1)
add_map(ax, ctx.providers.CartoDB.Positron, 0.0025)
ax = axes[2][1]
loc = lesser
draw_part_with_label(ax, loc[0], "right", loc[1], loc[2], loc[3], params1)
add_map(ax, ctx.providers.CartoDB.Positron, 0.0025)
🚈 Coverage by Transport Mode
This section visualizes the coverage area of selected transport types: buses, trams, trains, and metro.
def filter_dist(route, dist):
g = route_graph(conns, route)
H = nx.Graph()
H2 = nx.Graph()
l1 = []
for e1, e2 in g.edges:
p1 = stops.loc[e1].to_numpy()
p2 = stops.loc[e2].to_numpy()
if np.linalg.norm(p1 - p2) < dist:
l1.append((e1, e2))
H.add_edges_from(l1)
return H
def route_graph(cc, route_type):
H = nx.Graph()
h_edges = extract_edges(cc[cc["route_type"] == route_type])
H.add_weighted_edges_from(h_edges)
return H
fig, ax = plt.subplots(1, 1, figsize=(9, 9), layout="tight")
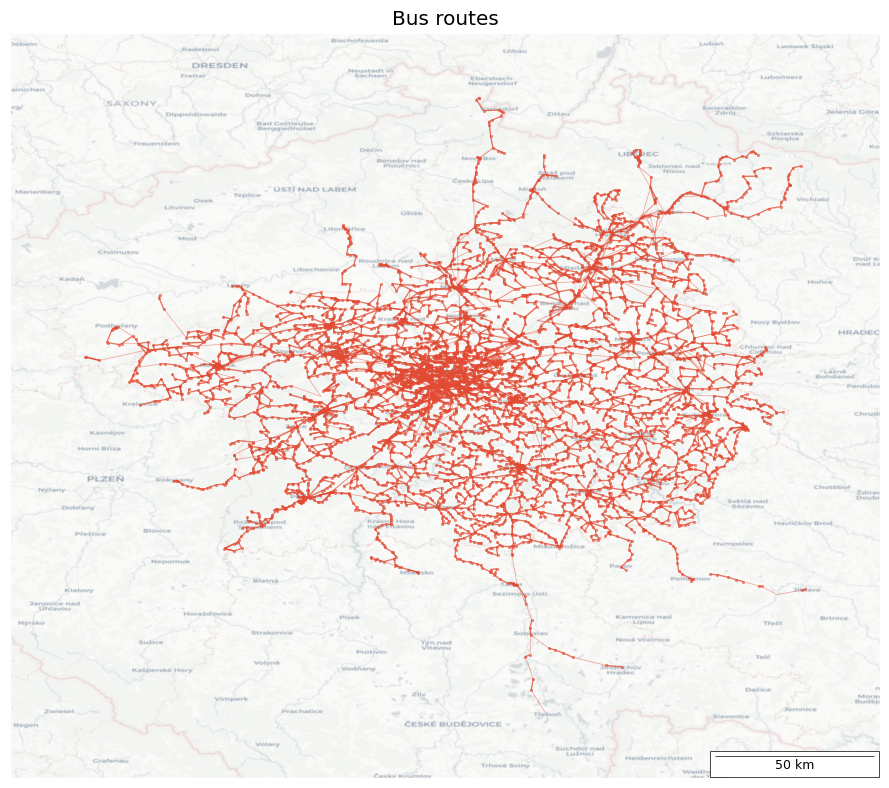
route = "Bus"
ax.set_title(f"{route} routes")
h1 = filter_dist(route, 0.05)
h2 = filter_dist(route, 0.15)
nx.draw_networkx(h2, pos=stop_pos, ax=ax, with_labels=False, node_size=0, node_color=redl, width=0.5, edge_color=redl, alpha=0.5)
nx.draw_networkx(h1, pos=stop_pos, ax=ax, with_labels=False, node_size=3, node_color=redl, width=1, edge_color=redl)
add_map(ax, ctx.providers.Esri.WorldGrayCanvas, 0.5)
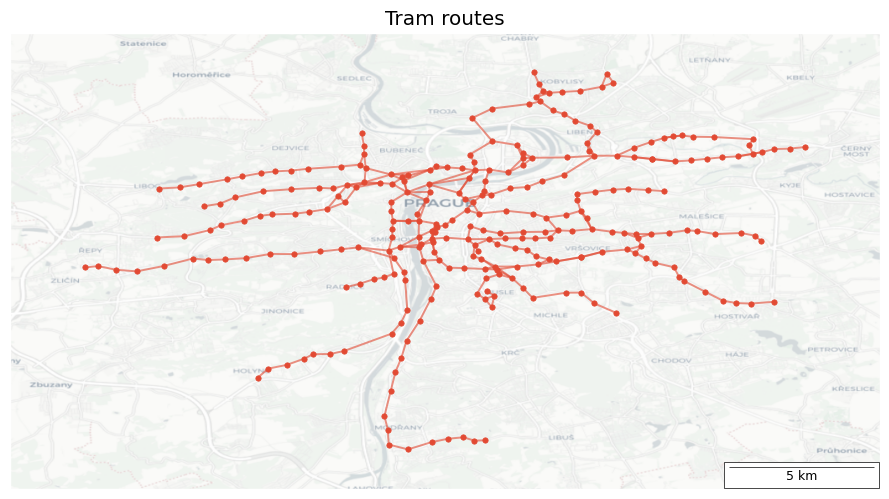
fig, ax = plt.subplots(1, 1, figsize=(9, 9), layout="tight")
route = "Tram"
ax.set_title(f"{route} routes")
nx.draw_networkx(route_graph(conns, route), pos=stop_pos, ax=ax, with_labels=False, node_size=15, node_color=redf, width=1.4, edge_color=redl)
add_map(ax, ctx.providers.Esri.WorldGrayCanvas, 0.05)
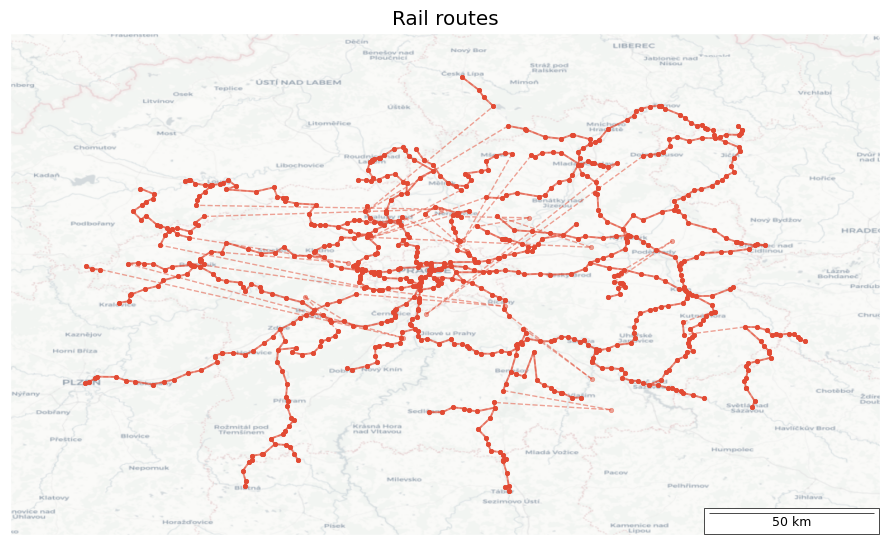
fig, ax = plt.subplots(1, 1, figsize=(9, 9), layout="tight")
route = "Rail"
ax.set_title(f"{route} routes")
h1 = filter_dist(route, 0.1)
h2 = filter_dist(route, 1)
nx.draw_networkx(h2, pos=stop_pos, ax=ax, with_labels=False, node_size=10, node_color=redf, width=1, edge_color=redl, alpha=0.5, style="dashed")
nx.draw_networkx(h1, pos=stop_pos, ax=ax, with_labels=False, node_size=10, node_color=redf, width=1.4, edge_color=redl)
add_map(ax, ctx.providers.Esri.WorldGrayCanvas, 0.5)
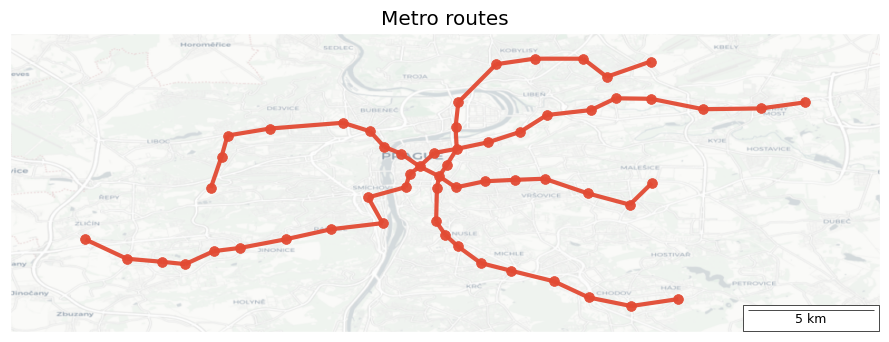
fig, ax = plt.subplots(1, 1, figsize=(9, 9), layout="tight")
route = "Metro"
ax.set_title(f"{route} routes")
nx.draw_networkx(route_graph(conns, route), pos=stop_pos, ax=ax, with_labels=False, node_size=50, node_color=redf, width=3, edge_color=redf, alpha=0.95)
add_map(ax, ctx.providers.Esri.WorldGrayCanvas, 0.05)
📝 Notes
- Of the transport modes shown, buses and trams have the densest lines, considering the scale.
- Prague Integrated Transport (PID) covers a significant part of the Czech Republic, not just Prague.
The Rail routes graph shows short connections (<10 km) with solid lines, long connections (<110 km) with dashed lines, and connections longer than 110 km are not displayed.
📊 Node Analysis
Node analysis is performed using centrality measures. The following visualization displays selected stop centralities in the center of Prague.
A deeper node analysis will then be performed on the entire PID network.
def make_plotter(g, lbc, urc):
# https://stackoverflow.com/a/67230951/13022894
def plot_centrality(ax, centrality, *, label_count=0, **kwargs):
ax.set_title(centrality.__name__)
ax.set_xlim(lbc[1], urc[1])
ax.set_ylim(lbc[0], urc[0])
deg_cent = centrality(g, **kwargs)
degree_centrality = pd.Series(deg_cent).sort_values(ascending=False)
colors = degree_centrality / np.max(degree_centrality) * 5000
cent = np.fromiter(deg_cent.values(), float)
normalize = mcolors.Normalize(vmin=cent.min(), vmax=cent.max())
scalarmappaple = cm.ScalarMappable(norm=normalize, cmap=colormap)
scalarmappaple.set_array(cent)
fig.colorbar(scalarmappaple, ax=ax)
colors = cent / np.max(cent) * 200
nx.draw(g, stop_pos, ax=ax, node_size=colors, node_color=colors, cmap=colormap, edge_color=grey, width=0.6)
nx.draw_networkx_labels(g.subgraph(degree_centrality[:label_count].index), stop_pos, ax=ax, verticalalignment='bottom')
add_map(ax, ctx.providers.Esri.WorldGrayCanvas, 0.01)
return plot_centrality
fig, axes = plt.subplots(2, 2, figsize=(13, 9), layout="constrained")
fig.suptitle("Network centralities - Centre of Prague", fontsize=20)
colormap = cm.YlOrRd
g = filter_d((np.array(centre[1]) + np.array(centre[2])) / 2, 0.1)
plot_centrality = make_plotter(g, centre[1], centre[2])
plot_centrality(axes[0][0], nx.degree_centrality, label_count=1)
plot_centrality(axes[0][1], nx.closeness_centrality)
plot_centrality(axes[1][0], nx.eigenvector_centrality, weight="weight", label_count=2)
plot_centrality(axes[1][1], nx.betweenness_centrality, weight="weight", label_count=6)
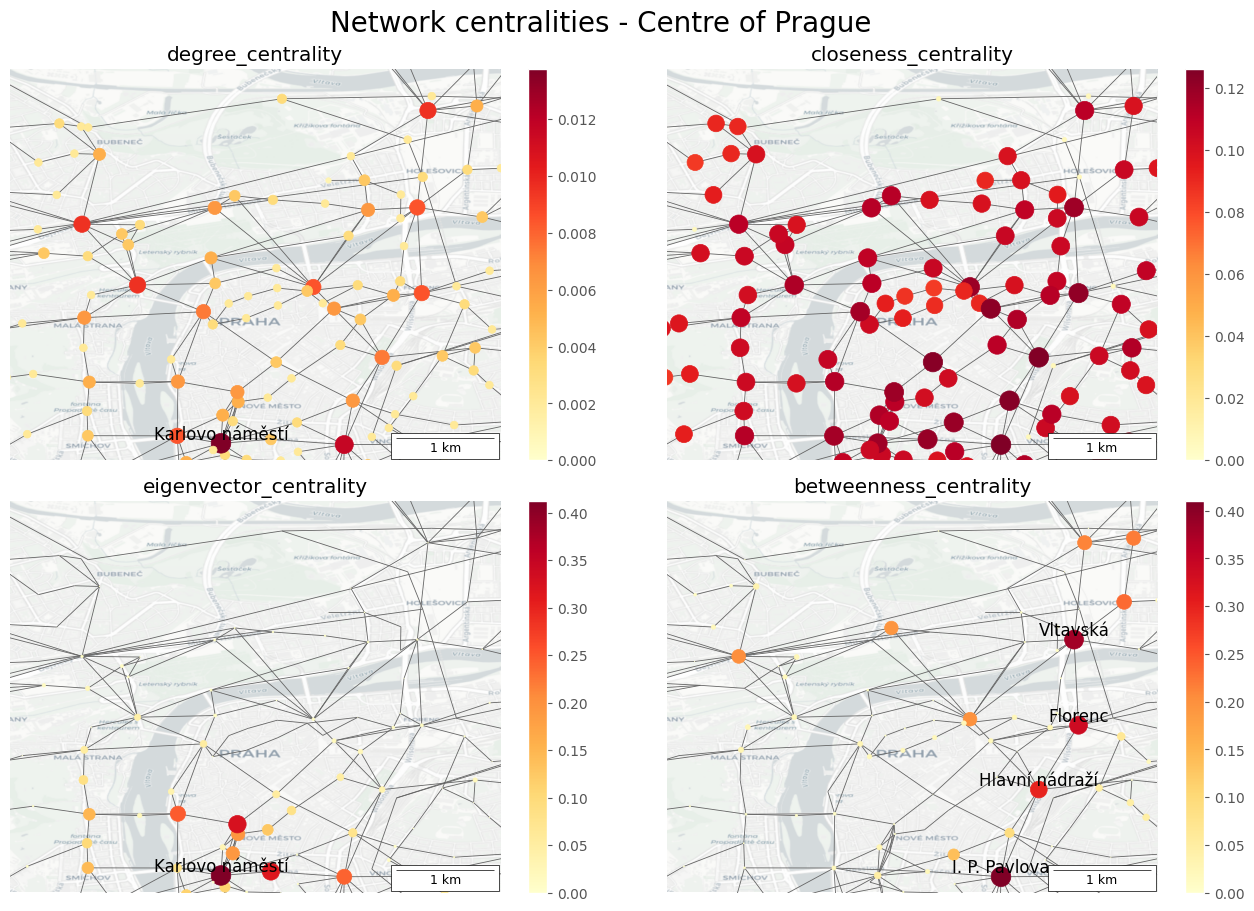
🗨️ Interpreting Centralities in Prague Centre
🌡️ Degree Centrality
- The metro stations show the highest significance by degree, acting as hubs/authorities in the transport network.
📐 Closeness Centrality
- In the dense center of Prague, all stops are significant in terms of closeness centrality.
⚖️ Eigenvector Centrality (Weighted Edges)
- This centrality indicates that Karlovo náměstí metro station is a very important node in this part of Prague, with a strong influence on its neighbors.
- (It quantifies the overall importance of nodes, the importance of edges originating from them, and the importance of their neighbors.)
🖇️ Betweenness Centrality
- This metric provides information about the importance of individual nodes in relation to other shortest paths.
- The red metro line C is particularly interesting for this section, as most of the shortest connections flow through it.
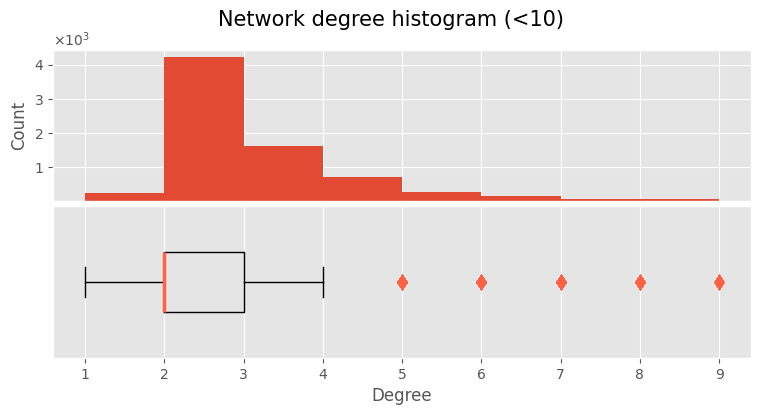
🌡️ Degree Centrality
This section focuses on analyzing degree centrality across the entire graph.
degrees = pd.Series([d for n, d in G.degree()])
degrees = degrees[degrees < 10]
fig, axes = plt.subplots(2, 1, figsize=(9, 4), sharex=True)
fig.suptitle("Network degree histogram (<10)", size=15)
ax = axes[0]
ax.hist(degrees, bins=(degrees.max() - degrees.min()).astype(int))
ax.ticklabel_format(axis="y", style="sci", scilimits=(0, 0), useMathText=True)
ax.set_yticks([1000, 2000, 3000, 4000])
ax.set_ylabel("Count")
ax.tick_params(labelbottom=False)
ax.tick_params(axis="x", which="both", length=0)
medianprops = dict(linewidth=2.5, color=(1, 0.38, 0.27))
flierprops = dict(marker="d", markerfacecolor=(1, 0.38, 0.27), markersize=8, markeredgecolor="none")
ax = axes[1]
ax.boxplot(degrees, vert=False, widths=[0.4], showfliers=True, flierprops=flierprops, medianprops=medianprops)
ax.get_yaxis().set_visible(False)
ax.set_xlabel("Degree")
fig.subplots_adjust(hspace=0.03)
def display_top(ps):
df = pd.DataFrame(ps, columns=["Coeff"])
styler = df.style.format(precision=7, thousands=" ", decimal=".")
display(styler)
degree_centrality = pd.Series(nx.degree_centrality(G)).sort_values(ascending=False)
top10 = degree_centrality[:10]
print("Top 10 nodes with the highest degree centrality")
display_top(top10)
neighbours = set()
for n in top10.index:
for u in nx.all_neighbors(G, n):
neighbours.add(u)
for _ in range(3):
nn = neighbours.copy()
for n in nn:
for u in nx.all_neighbors(G, n):
neighbours.add(u)
cumulative = list(neighbours)
cumulative.extend(list(top10.index))
len(cumulative)
fig, ax = plt.subplots(1, 1, figsize=(12, 7), layout="constrained")
fig.suptitle("10 nodes with the highest degree centrality and their 3-neighbourhood", fontsize=15)
nx.draw_networkx(G.subgraph(cumulative), pos=stop_pos, ax=ax, node_size=10, node_color=blue, with_labels=False, alpha=0.1, edge_color=blue, width=1)
nx.draw_networkx(G.subgraph(top10.index), pos=stop_pos, ax=ax, node_size=50, node_color=redl, font_size=10, width = 0)
add_map(ax, ctx.providers.CartoDB.Positron, 0.5, False)
A = [49.5568518946815, 13.510323360859733]
B = [50.709352011905555, 15.35150400382775]
ax.set_xlim(A[1], B[1])
ax.set_ylim(A[0], B[0]);
Top 10 nodes with the highest degree centrality
| Coeff | |
|---|---|
| Zličín | 0.0022995 |
| Lihovar | 0.0021642 |
| Černý Most | 0.0020289 |
| Mladá Boleslav,aut.st. | 0.0018937 |
| Kladno,Pražská křiž. | 0.0017584 |
| Chrášťany | 0.0017584 |
| Karlovo náměstí | 0.0017584 |
| Jesenice | 0.0016232 |
| Kobylisy | 0.0016232 |
| Turnov,Terminál u žel.st. | 0.0016232 |
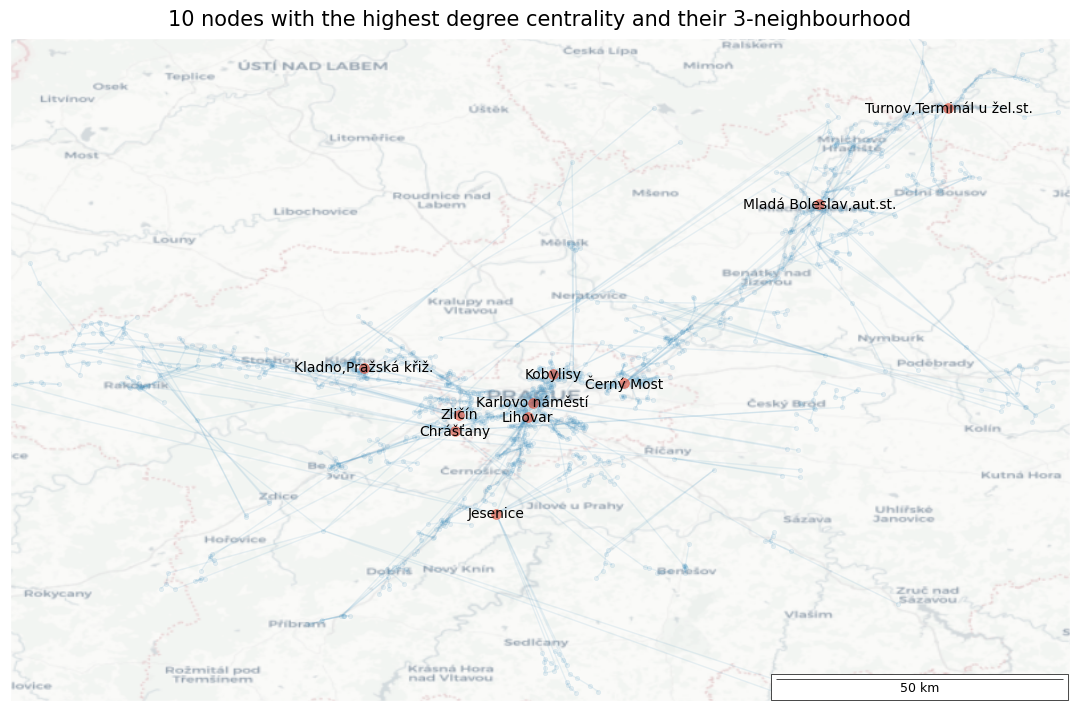
📝 Description
Nodes with the highest degree centrality are primarily large bus terminals. Connections from these nodes typically extend outside Prague, which is characteristic of bus hubs.
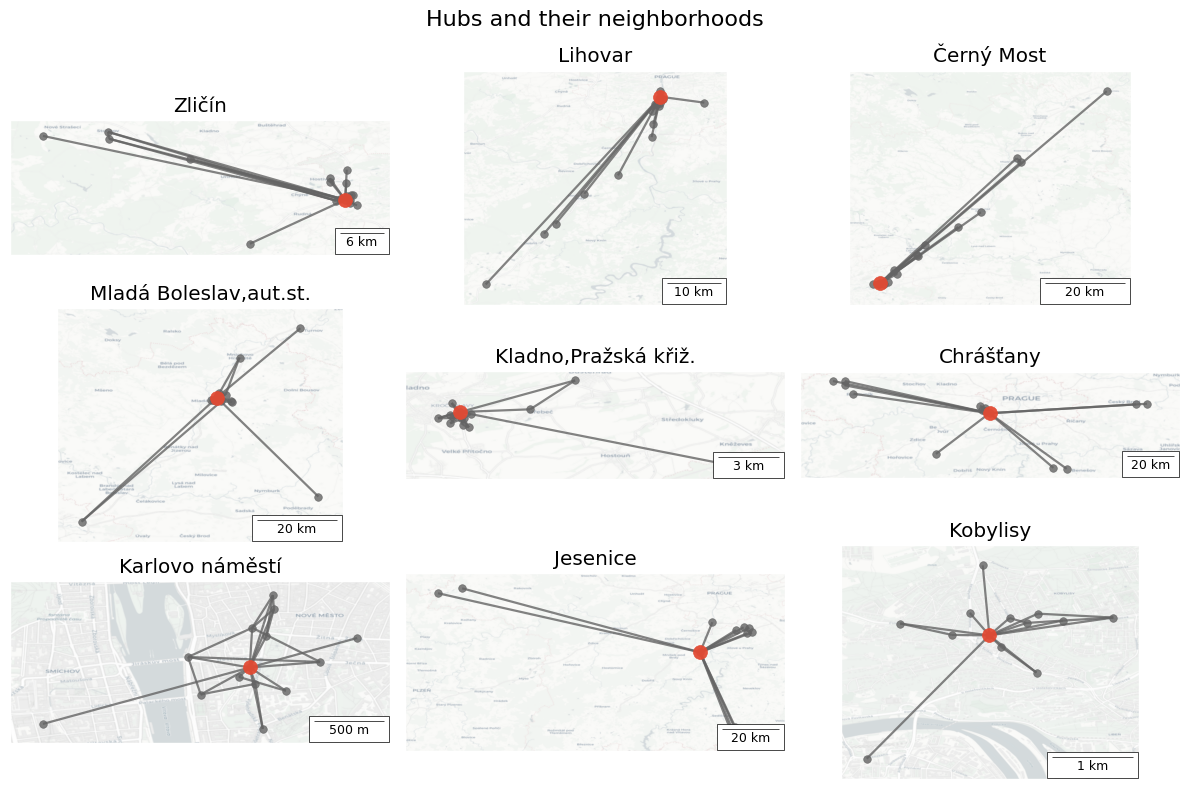
🏠 Neighborhood
The following maps visualize the immediate neighbors of these highly central nodes. With a few exceptions, these nodes’ neighbors are quite distant.
fig, axes = plt.subplots(3, 3, figsize=(12, 8), layout="tight")
fig.suptitle("Hubs and their neighborhoods", fontsize=16)
scales = [0.06, 0.1, 0.2, 0.2, 0.03, 0.2, 0.005, 0.2, 0.01]
for node, ax, scale in zip(top10.index[:9], axes.reshape(-1), scales):
neighbours = set([node])
for u in nx.all_neighbors(G, node):
neighbours.add(u)
ax.set_title(node)
nx.draw_networkx(G.subgraph(neighbours), pos=stop_pos, ax=ax, node_size=30, node_color=grey,
with_labels=False, alpha=0.8, edge_color=grey, width=1.6)
nx.draw_networkx(G.subgraph([node]), pos=stop_pos, ax=ax, node_size=100, node_color=redf, alpha=0.95, with_labels=False)
add_map(ax, ctx.providers.CartoDB.Positron, scale, True)
📐 Closeness Centrality
centrality = pd.Series(nx.closeness_centrality(G)).sort_values(ascending=False)
lbc = [50.03774851490303, 14.331014307052019]
urc = [50.13010922185579, 14.500335441536306]
nodes = filter(lbc, urc)
f = centrality[list(nodes)].sort_values(ascending=False)
f = f.drop('Nad Pahorkem')
f = f.drop('Choceradská')
top10 = f[1:11]
print("Top 10 nodes with the highest closeness centrality")
display_top(top10)
neighbours = set()
for n in top10.index:
for u in nx.all_neighbors(G, n):
neighbours.add(u)
for _ in range(10):
nn = neighbours.copy()
for n in nn:
for u in nx.all_neighbors(G, n):
neighbours.add(u)
cumulative = list(neighbours)
cumulative.extend(list(top10.index))
len(cumulative)
fig, ax = plt.subplots(1, 1, figsize=(12, 6), layout="constrained")
fig.suptitle("10 nodes with the highest closeness centrality", fontsize=15)
ax.set_xlim(lbc[1], urc[1])
ax.set_ylim(lbc[0], urc[0])
nx.draw_networkx(G.subgraph(cumulative), pos=stop_pos, ax=ax, node_size=10, node_color=blue, with_labels=False, alpha=0.2, edge_color=blue, width=1)
nx.draw_networkx(G.subgraph(top10.index), pos=stop_pos, ax=ax, node_size=150, node_color=redl, font_size=10, width=0)
add_map(ax, ctx.providers.CartoDB.Positron, 0.01)
Top 10 nodes with the highest closeness centrality
| Coeff | |
|---|---|
| Kačerov | 0.0741755 |
| Na Veselí | 0.0740663 |
| Lihovar | 0.0734723 |
| Smíchovské nádraží | 0.0727514 |
| Hlavní nádraží | 0.0721860 |
| I. P. Pavlova | 0.0721479 |
| Budějovická | 0.0715759 |
| Pankrác | 0.0709528 |
| Radlická | 0.0704498 |
| Benkova | 0.0700958 |
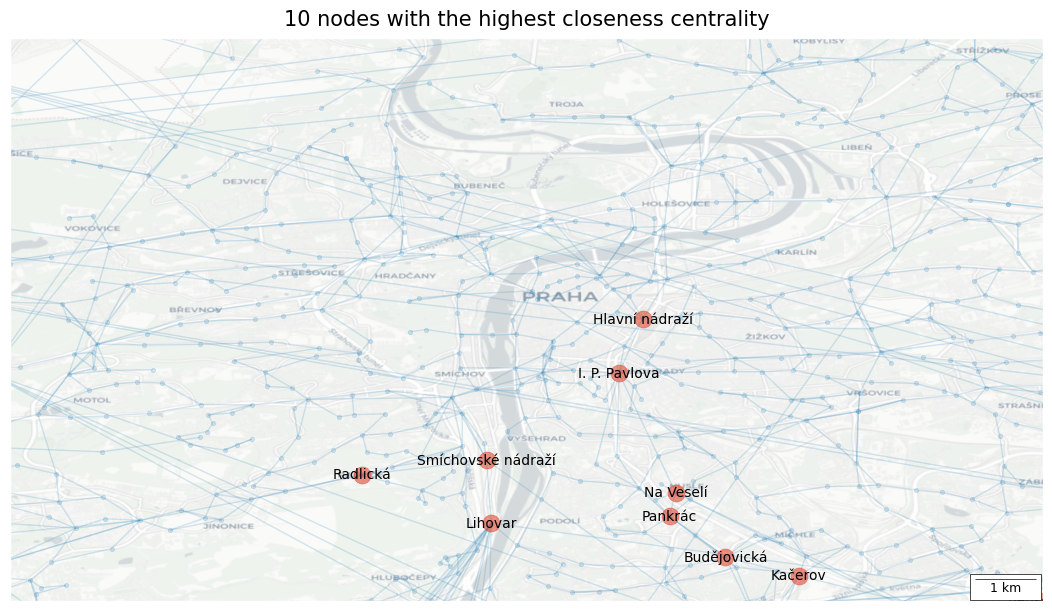
🗨️ Interpretation
The highlighted stops are crucial points in the PID transport network. They have the lowest average distance to all other stops.
🖇️ Betweenness Centrality
centrality_bet = pd.Series(nx.betweenness_centrality(G, weight="weight", k=200)).sort_values(ascending=False)
lbc = [50.03774851490303, 14.331014307052019]
urc = [50.13010922185579, 14.500335441536306]
nodes = filter(lbc, urc)
top10 = centrality_bet[list(nodes)].sort_values(ascending=False)[:10]
print("Top 10 nodes with highest betweeness centrality")
display_top(top10)
neighbours = set()
for n in top10.index:
for u in nx.all_neighbors(G, n):
neighbours.add(u)
for _ in range(10):
nn = neighbours.copy()
for n in nn:
for u in nx.all_neighbors(G, n):
neighbours.add(u)
cumulative = list(neighbours)
cumulative.extend(list(top10.index))
len(cumulative)
fig, ax = plt.subplots(1, 1, figsize=(12, 6), layout="constrained")
fig.suptitle("10 nodes with the highest betweeness centrality", fontsize=15)
ax.set_xlim(lbc[1], urc[1])
ax.set_ylim(lbc[0], urc[0])
nx.draw_networkx(G.subgraph(cumulative), pos=stop_pos, ax=ax, node_size=10, node_color=blue, with_labels=False, alpha=0.2, edge_color=blue, width=1)
nx.draw_networkx(G.subgraph(top10.index), pos=stop_pos, ax=ax, node_size=150, node_color=redl, font_size=10, width=0)
add_map(ax, ctx.providers.CartoDB.Positron, 0.01)
Top 10 nodes with highest betweeness centrality
| Coeff | |
|---|---|
| Na Veselí | 0.0889256 |
| I. P. Pavlova | 0.0714338 |
| Botanická zahrada Troja | 0.0397029 |
| Hlavní nádraží | 0.0388959 |
| Pankrác | 0.0383901 |
| Střížkov | 0.0383537 |
| Poliklinika Budějovická | 0.0358492 |
| Zoologická zahrada | 0.0336205 |
| Parkoviště Trojský most | 0.0325963 |
| Prosek | 0.0313351 |
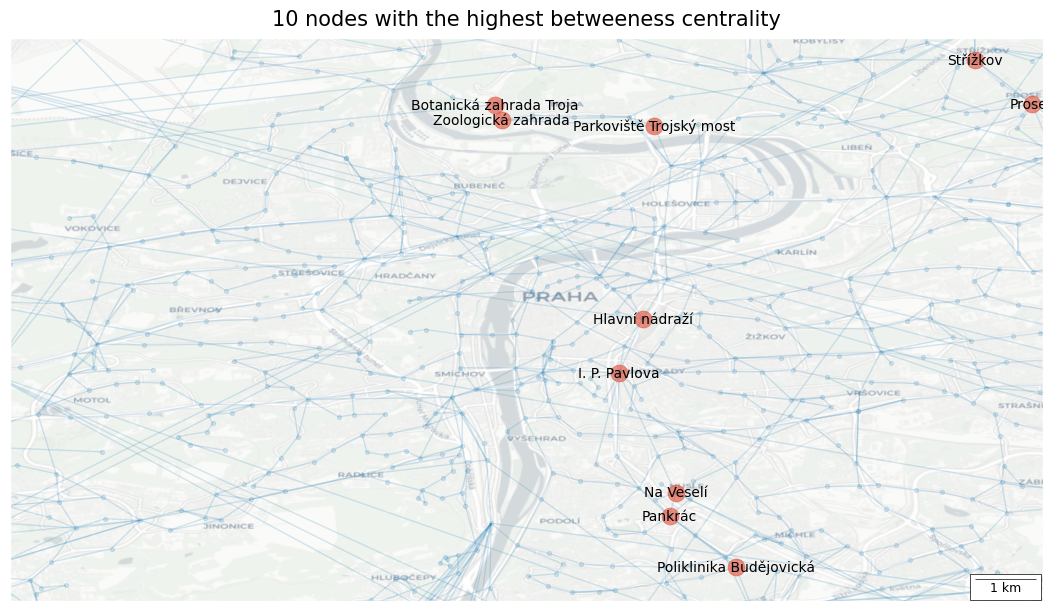
🗨️ Interpretation
The highlighted stops are frequently part of the shortest paths between other pairs of nodes.
❓ Insights
How does transport frequency change between weekdays and weekends, and across different transport types?
fig, axes = plt.subplots(6, figsize=(9, 10), sharex=True)
fig.suptitle(f"Activity by Route Types", y=0.92, fontsize=16)
fig.subplots_adjust(hspace=0.08)
fig.text(0.5, 0.04, "Time [hour]", ha="center", size=12)
fig.text(0.04, 0.5, "Count", va="center", rotation="vertical", size=12)
for route_type, ax in zip(types.index, fig.axes):
d = conns[(conns["route_type"] == route_type) & (conns["monday"] | conns["tuesday"] | conns["wednesday"] | conns["thursday"] | conns["friday"])]
series = d["depart_from_H"] * 3600 + d["depart_from_M"] * 60 + d["depart_from_S"]
series = series / 3600
n, _, _ = ax.hist(series, bins=48, alpha=0.8)
ax.set_title(f"{route_type}", y=1.0, pad=-14, loc="left", color=grey)
ax.set_yticks([0, max(n) * 2 / 4, max(n)])
ax.set_ylim(0, max(n) * 1.4)
ax.tick_params(axis="y", which="both", length=0)
ax.grid(which="major", axis="x", color="grey", linestyle="dotted", linewidth=0.4)
d = conns[(conns["route_type"] == route_type) & (conns["saturday"] | conns["saturday"])]
series = d["depart_from_H"] * 3600 + d["depart_from_M"] * 60 + d["depart_from_S"]
series = series / 3600
n, _, _ = ax.hist(series, bins=48, color="k", histtype="step", linewidth=1, alpha=0.8)
handles, labels = plt.gca().get_legend_handles_labels()
patch = mpatches.Patch(color=red, label="Weekday", alpha=0.8)
line = Line2D([0], [0], label="Weekend", color="k", linewidth=1)
handles.extend([patch, line])
axes[0].legend(handles=handles, bbox_to_anchor=(1.04, 1), loc="upper left", prop={'size': 12})
ax.set_xticks(range(0, 25, 4))
ax.set_xlim(-1, 25);
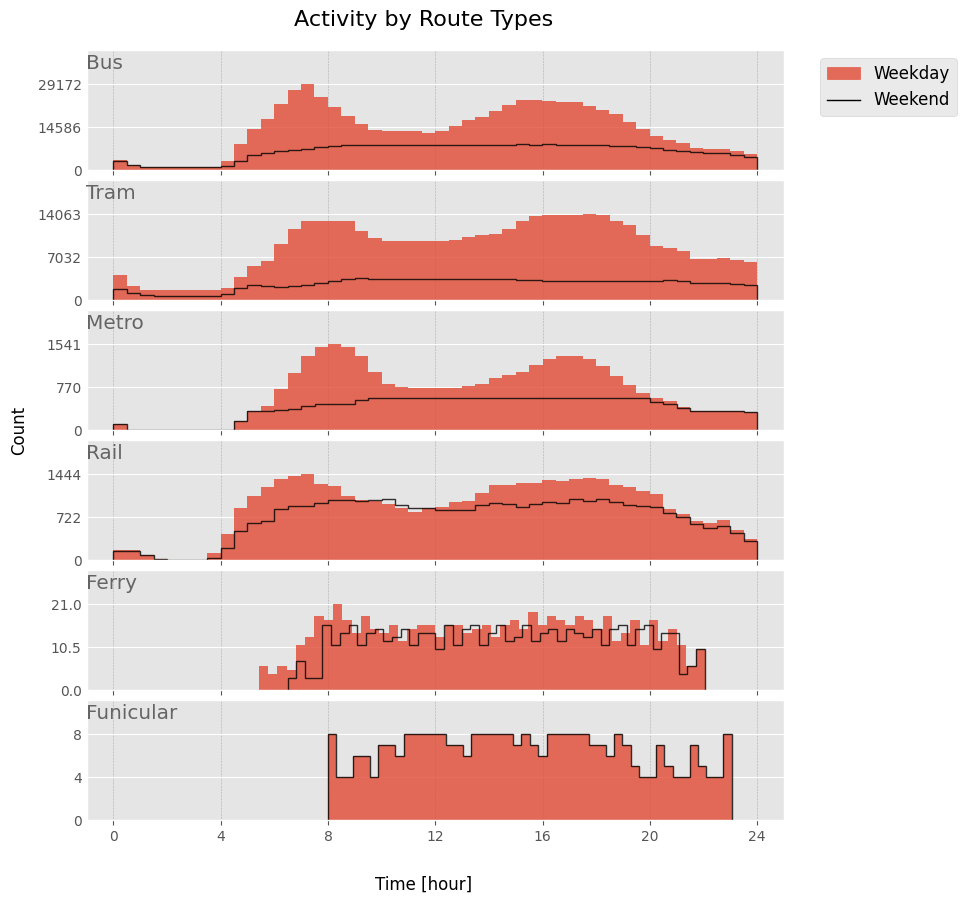
🗨️ Interpretation
- Transport activity is significantly lower on weekends. The exceptions are ferries and the funicular, which operate similarly on weekends. Metro and train frequencies are also comparable to weekdays outside of peak hours.
- On weekdays, there are more connections during morning and evening rush hours, aligning with commuter travel patterns. This adaptation is not observed on weekends.
- Overall, the frequency of connections is very low between 11 PM and 4 AM. For ferries and the funicular, it’s zero.
Do important stops change between day and night operations?
For this question, stop importance is analyzed using degree centrality.
G_weekday = build_graph(conns[conns['monday'] | conns['tuesday'] | conns['wednesday'] | conns['thursday'] | conns['friday']])
filter_d_weekday = subgroup_distance_filter(G_weekday, stops)
G_weekend = build_graph(conns[conns['saturday'] | conns['sunday']])
filter_d_weekend = subgroup_distance_filter(G_weekend, stops)
G_day = build_graph(conns[~conns['is_night']])
filter_d_day = subgroup_distance_filter(G_day, stops)
G_night = build_graph(conns[conns['is_night']])
filter_d_night = subgroup_distance_filter(G_night, stops)
loc = ['', [50.04909793668076, 14.379518399273855], [50.112147437060834, 14.481384833754964], 0.4]
fig, axes = plt.subplots(2, 1, figsize=(10, 12), layout="constrained")
fig.suptitle("Degree centrality - Central Prague", fontsize=20)
g = filter_d_day((np.array(loc[1]) + np.array(loc[2])) / 2, loc[3])
plot_centrality = make_plotter(g, loc[1], loc[2])
plot_centrality(axes[0], nx.degree_centrality, label_count=18)
axes[0].set_title("Daytime")
g = filter_d_night((np.array(loc[1]) + np.array(loc[2])) / 2, loc[3])
plot_centrality = make_plotter(g, loc[1], loc[2])
plot_centrality(axes[1], nx.degree_centrality, label_count=5)
axes[1].set_title("Nighttime");
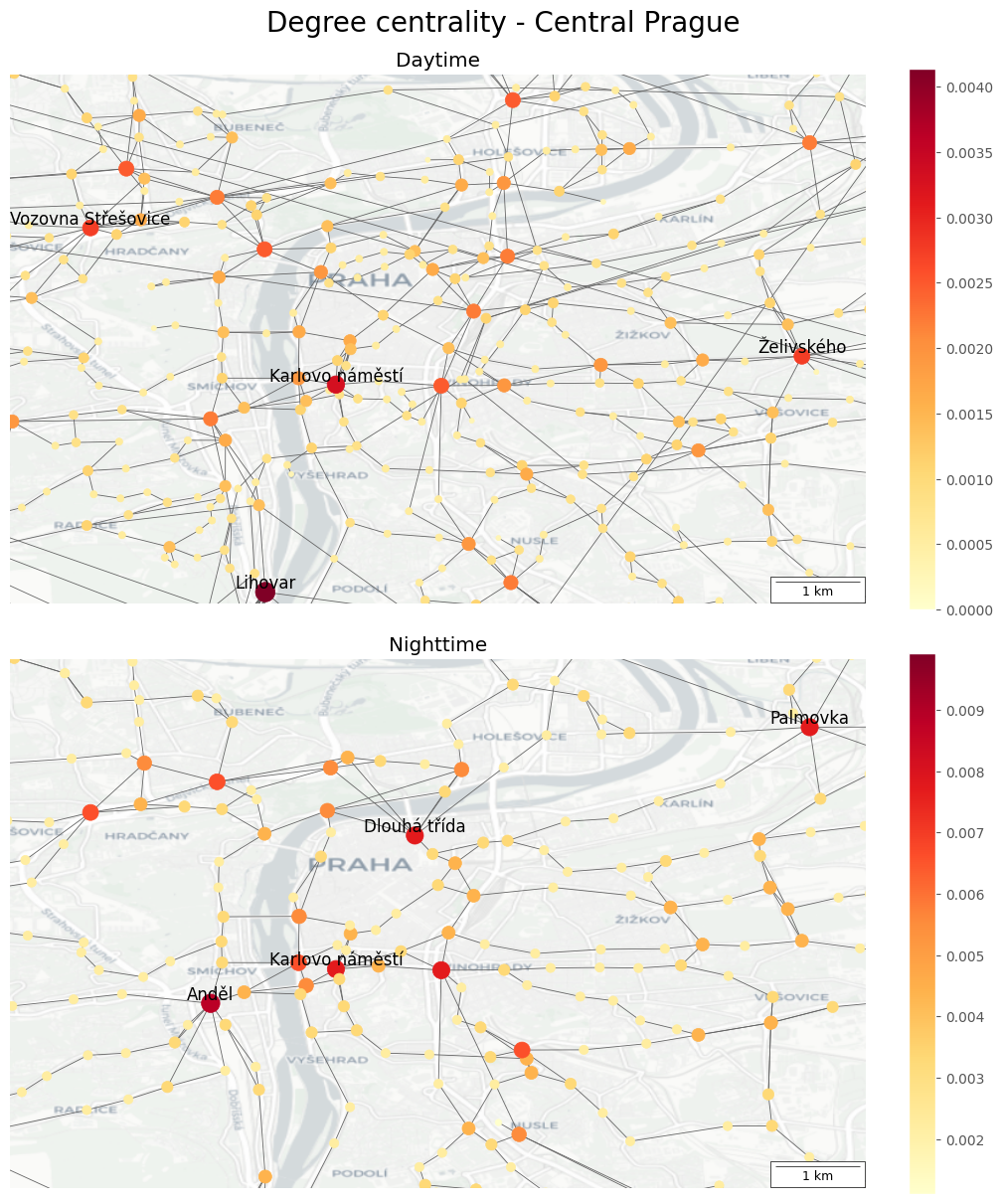
🗨️ Interpretation
Yes, the importance of stops changes between day and night operations. For example, Lihovar, which is the most important stop by degree centrality during the day, is insignificant during night operations. Conversely, Anděl station becomes more significant at night.
Which out-of-Prague stops are the busiest?
As in the previous question, importance is again assessed by degree centrality.
mid = [50.089027446744275, 14.420374242931851]
g = filter_d_inv(mid, 0.2)
H = g.copy()
H.remove_node('Kladno,Pražská křiž.')
H.remove_node('Mladá Boleslav,Jičínská')
g = H
deg_cent = nx.degree_centrality(g)
degree_centrality = pd.Series(deg_cent).sort_values(ascending=False)
n = 6
top = degree_centrality[:n]
print(f"Top {n} nodes with the highest degree centrality")
display_top(top)
fig, ax = plt.subplots(1, 1, figsize=(14, 10), layout="constrained")
fig.suptitle(f"{n} nodes with the highest degree centrality (outside of Prague)", fontsize=16)
colors = degree_centrality / np.max(degree_centrality)
cent = np.fromiter(deg_cent.values(), float)
normalize = mcolors.Normalize(vmin=cent.min(), vmax=cent.max())
scalarmappaple = cm.ScalarMappable(norm=normalize, cmap=colormap)
scalarmappaple.set_array(cent)
fig.colorbar(scalarmappaple, ax=ax)
colors = cent / np.max(cent) * 200
nx.draw(g, stop_pos, ax=ax, node_size=colors*0.4, node_color=colors, cmap=colormap, width=0, alpha=0.4)
indices = []
for n, v in top.items():
indices.append(pd.Index(g.nodes).get_loc(n))
nx.draw_networkx_nodes(g.subgraph(top.index), stop_pos, ax=ax, node_size=colors[indices]*0.3, node_color=redf, alpha=0.4)
nx.draw_networkx_labels(g.subgraph(top.index), stop_pos, ax=ax, verticalalignment='bottom', font_size=11)
add_map(ax, ctx.providers.CartoDB.Positron, 0.5)
Top 6 nodes with the highest degree centrality
| Coeff | |
|---|---|
| Mladá Boleslav,aut.st. | 0.0021771 |
| Kladno,autobusové nádraží | 0.0019956 |
| Mšeno | 0.0019956 |
| Turnov,Terminál u žel.st. | 0.0019956 |
| Říčany,K Žel.st. | 0.0019956 |
| Mutějovice | 0.0018142 |
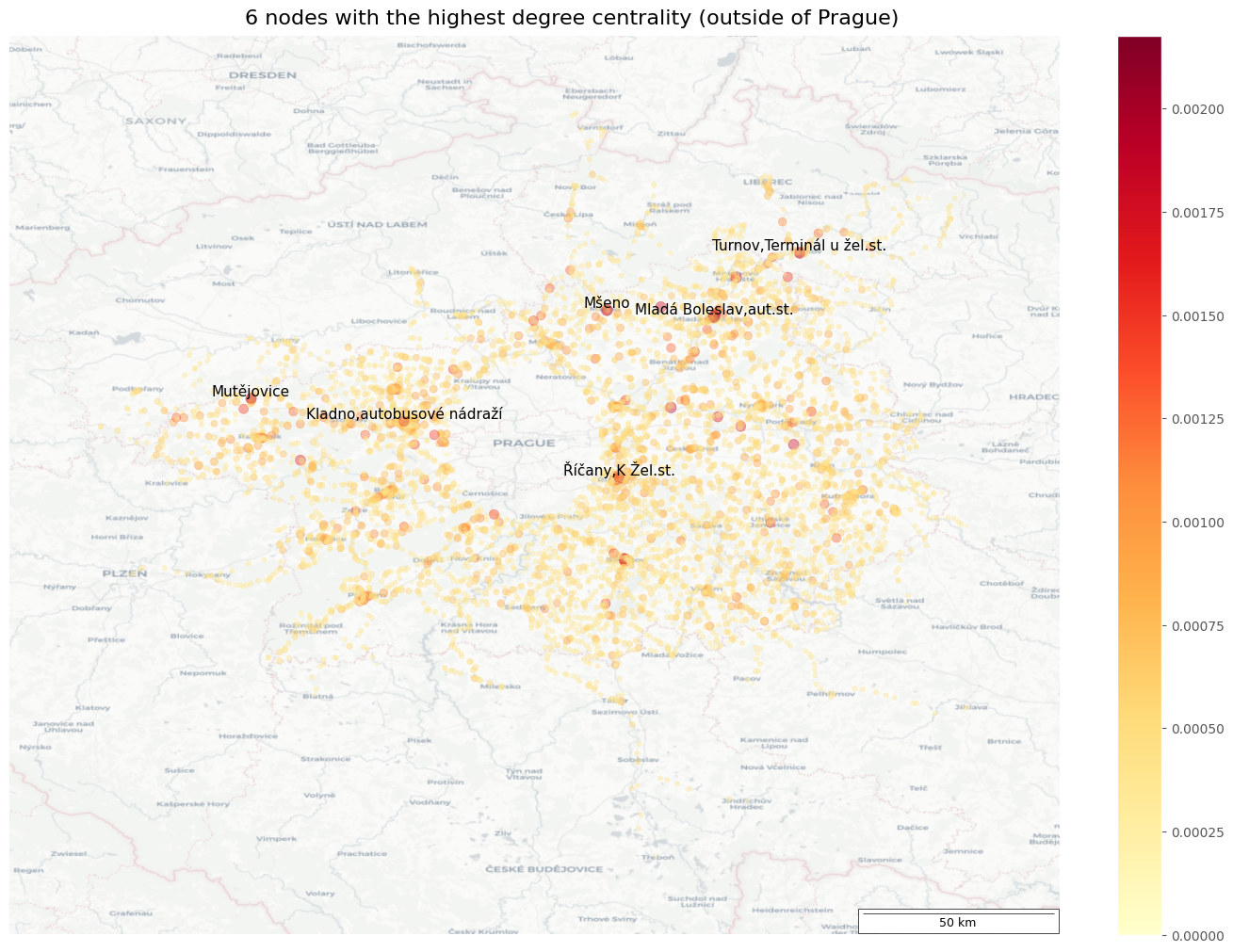
🗨️ Interpretation
Similar to the overall graph’s degree centrality, the most important stops outside of Prague are large bus stations.
Which stops are most significant during weekday mornings (6:00 - 11:00 AM)?
conns_morning = (conns['depart_from_H'] >= 6) & (conns['depart_from_H'] <= 11)
conns_weekday = (conns['monday'] | conns['tuesday'] | conns['wednesday'] | conns['thursday'] | conns['friday'])
G_morning_weekday = build_graph(conns[conns_morning & conns_weekday])
filter_d_mwd = subgroup_distance_filter(G_morning_weekday, stops)
g = filter_d_mwd(mid, 0.02)
deg_cent = nx.eigenvector_centrality(g, weight="weight", max_iter=1000)
degree_centrality = pd.Series(deg_cent).sort_values(ascending=False)
n = 15
top = degree_centrality[:n]
print(f"Top {n} nodes with the highest eigenvector centrality")
display_top(top)
fig, ax = plt.subplots(1, 1, figsize=(12, 10), layout="constrained")
fig.suptitle(f"{n} nodes with the highest eigenvector centrality on weekday morning", fontsize=16)
colors = degree_centrality / np.max(degree_centrality)
cent = np.fromiter(deg_cent.values(), float)
# normalize = mcolors.Normalize(vmin=cent.min(), vmax=cent.max())
# scalarmappaple = cm.ScalarMappable(norm=normalize, cmap=colormap)
# scalarmappaple.set_array(cent)
# fig.colorbar(scalarmappaple, ax=ax)
colors = cent / np.max(cent) * 200
nx.draw(g, stop_pos, ax=ax, node_size=colors*0.4, node_color=colors, cmap=colormap, width=0, alpha=0.6)
indices = []
for n, v in top.items():
indices.append(pd.Index(g.nodes).get_loc(n))
nx.draw_networkx_nodes(g.subgraph(top.index), stop_pos, ax=ax, node_size=colors[indices]*0.3, node_color=redf, alpha=0.8)
nx.draw_networkx_labels(g.subgraph(top.index), stop_pos, ax=ax, verticalalignment='bottom', font_size=11)
add_map(ax, ctx.providers.CartoDB.Positron, 0.01, False)
Top 15 nodes with the highest eigenvector centrality
| Coeff | |
|---|---|
| Karlovo náměstí | 0.4855651 |
| Národní třída | 0.4425812 |
| Štěpánská | 0.3632039 |
| Národní divadlo | 0.3594138 |
| Novoměstská radnice | 0.2402880 |
| Lazarská | 0.2090533 |
| Újezd | 0.2071608 |
| I. P. Pavlova | 0.2038303 |
| Moráň | 0.1490697 |
| Vodičkova | 0.1294884 |
| Hellichova | 0.1234722 |
| Palackého náměstí | 0.1125779 |
| Malostranské náměstí | 0.0819371 |
| Václavské náměstí | 0.0787817 |
| Staroměstská | 0.0783107 |
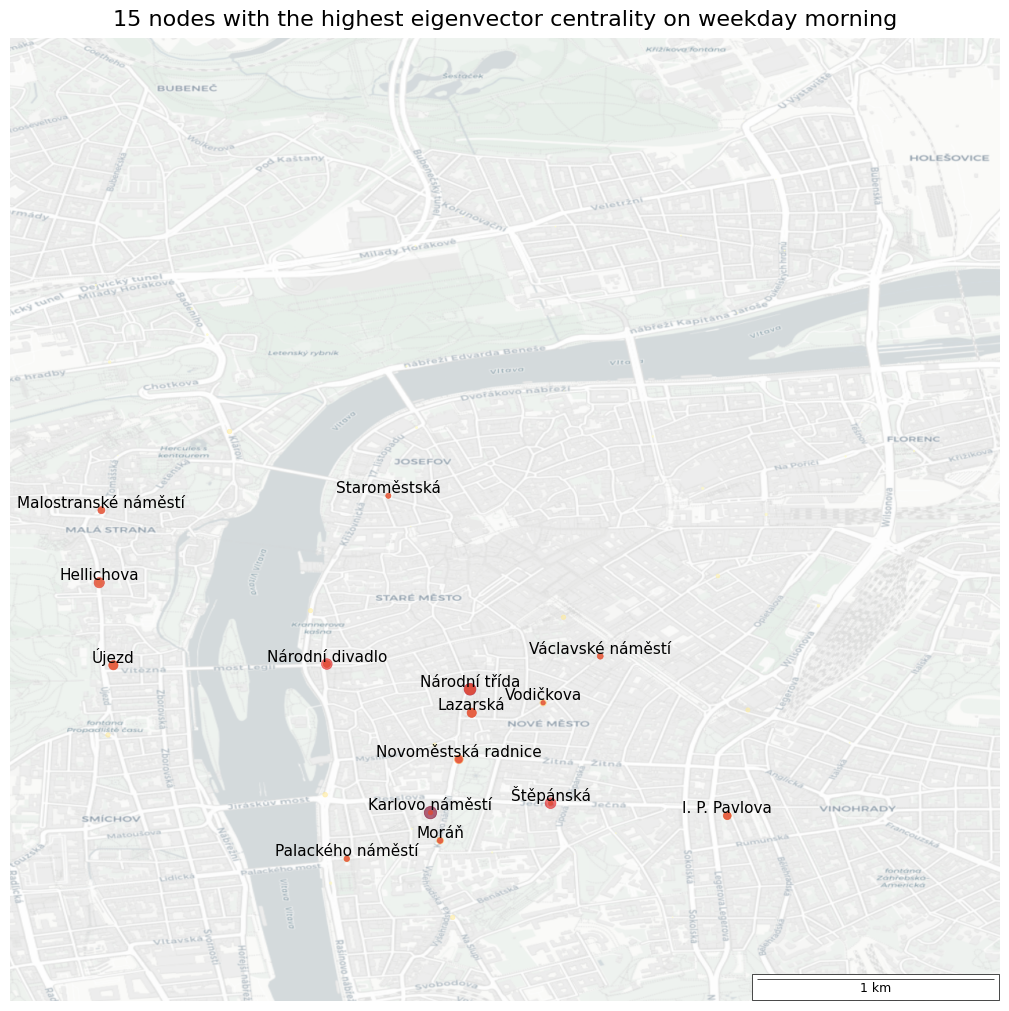
🗨️ Interpretation
The highlighted stops are the most significant on weekday mornings (6:00 AM - 11:00 AM). In the PID network, they connect influential nodes and form a crucial part of important connections.
Open Data Attribution
Copyright and license for the openly available geographical data used in the visualizations:
- OpenStreetMap® - licensed under the Open Data Commons Open Database License by the OpenStreetMap Foundation
- ArcGIS Online - licensed under the Esri Master License Agreement